动态规划DP

“你欺骗了我！作为惩罚，你必将重复徒劳而无意义的工作，直到永远！”，死神对西西弗斯说。

重复一件已经知道答案的事情有意义么？当然没有，所以我们要记住曾经已经解决的问题的答案，而不是像西西弗斯那样，做没有意义的工作，这就是动态规划算法的作用。

什么是动态规划？

动态规划涉及两种思想：递归和记忆，通过递归，大的问题被拆分（关于递归的讲解可以参考我的另一篇博客：）；通过记忆，以前被解决的问题的答案直接拿来用即可，避免了重复计算。（如果只是用传统递归，会有很多中间过程被重复进行）

动态规划解决什么问题？

优化问题：寻找最优解
组合问题：寻找可能的解决方案的组合，或者事件发生概率
子序列类型问题：子序列类型问题很难穷举，而动态规划所做的工作即为穷举+减枝，所以涉及子序列的问题基本都可以用动态规划进行解决。

动态优化框架

大问题可以拆分为子问题
通过子问题的最优解，递归地解决大问题
解决方式为自下而上
根据已经获得的信息构建最优解

（什么是自下而上？解决小问题，然后把它们组合起来解决大问题）

动态规划的一个关键点就是找到子问题以及初始条件，类似于科学归纳法，动态规划一定要找到几个初始条件的解。

确定初始条件
确定DP数组的含义，即要保存什么中间结果
确定递推公式
确定返回值

算法优缺点

优点：不容易超过规定内存大小

缺点：必须找到一个有效的解决问题的顺序

DP延伸算法

状态压缩DP

数位DP

DP难点总结

DP中最难的部分有两个

DP数组代表什么，即我们的状态是什么，我们要保存什么？
状态转移方程是什么，我们如何根据以前的结果推导现有的结果

本节将对常见的DP状态定义及转移方程进行总结。

一维DP

DP[i]的含义

DP[i]代表以vec[i]为结尾的某种状态

例题1：LeetCode 面试题42

输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

此时DP[i]代表以nums[i]结尾的连续子数组最大值。有了该定义，转移方程迎刃而解。

例题2：LeetCode 面试题 48 最长不含重复字符的子串

DP[i]就代表第i个要求的解

例题1：LeetCode 面试题49 丑数

我们把只包含因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

问题很好理解，后面的丑数一定是从前面某个数×2、×3或×5得到的，关键是究竟是哪一个数呢，这里采用了三指针法

设置三个指针p2,p3,p5
p2指向的数字下一次×2，p3指向的数字下一次×3，p5指向的数字×5
我们从$2×p_2,3×p_3,5×p_5$选取最小的一个数字，作为第k个丑数
如果第K个丑数==2×p2，也就是说前面0-p2个丑数×2不可能产生比第K个丑数更大的丑数了，所以p2++，p3,p5同理

状态转移方程

dp[i]的状态转移方程和前i个状态(dp[0] ~ dp[i-1])均可能有关

此时通常用一个变量保存前面所有状态中的某个最值。

279. 完全平方数

198. 打家劫舍

651. 4键键盘

假设你有一个特殊的键盘包含下面的按键：

Key 1: (A)：在屏幕上打印一个 ‘A’。

Key 2: (Ctrl-A)：选中整个屏幕。

Key 3: (Ctrl-C)：复制选中区域到缓冲区。

Key 4: (Ctrl-V)：将缓冲区内容输出到上次输入的结束位置，并显示在屏幕上。

现在，你只可以按键 N 次（使用上述四种按键），请问屏幕上最多可以显示几个 ‘A’呢？

令dp[i]为输入第i个键后A的数量，那么dp[i]最小为i，最大可能是由前面某个dp[i-k]经过复制得到的

32. 最长有效括号

给定一个只包含 '(' 和 ')' 的字符串，找出最长的包含有效括号的子串的长度。

思路

这个题DP的含义并不难想，就是以i结尾的子串的有效括号长度，难的是状态转移方程不好想，我们还是对这个问题给定具体例子，然后进行分析。假设当前字符串为s=")(())"，这个例子包含了非法括号，嵌套括号以及一般的配对括号。状态转移表如下：

	）	（	（	）	）
0	0	0	0	1	2
1		0	0	1	2
2			0	1	0
3				0	0
4					0

从上面的表中可以看出，凡是以’)’结尾的，有效括号长度均不会增加，因此不需考虑，只要看’)’结尾的情况，假设s[i]=')' && i>0，则又有如下几种情况：

如果s[i-1]='('，那么dp[i] = dp[i-2]+2
如果s[i-1]=')'，那么若s[i-dp[i-1]-1] = '('，说明`s[i-1]=和s[i-dp[i-1]-1]恰好能配对，从而dp[i] = dp[i-2]+2，但是这样还没结束，我们还要加上i-dp[i-1]-1前的有效括号长度，所以最后dp[i] = dp[i-2] + 2 + dp[i - dp[i-1] - 2]

代码

public int longestValidParentheses(String s) {
    int maxans = 0;
    int dp[] = new int[s.length()];
    for (int i = 1; i < s.length(); i++) {
        if (s.charAt(i) == ')') {
            if (s.charAt(i - 1) == '(') {
                dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
            } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
            }
            maxans = Math.max(maxans, dp[i]);
        }
    }
    return maxans;

dp[i]和前某几个状态有关

二维DP

DP[i]的含义

`DP[i][j]`表示条件为i，结果为j时的次数或最优解

例题1：LeetCode面试题60 n个骰子的点数

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

令dp[i][j]为i个骰子扔在地上，结果为j时的次数，那么dp[i][j] = dp[i-1][j-1]+dp[i-1][j-2]+…+dp[i-1][j-6]（当j大于6时，否则只加到dp[i-1][j-6]

例题2：LeetCode120. 三角形最小路径和

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。例如，给定三角形

[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]

自顶向下最小路径为(2+3+5+1 == 11)

令dp[i][j]表示包含nums[i][j]的最小路径和，那么dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1])+nums[i][j]，(当j为边界时特殊讨论)

`DP[i][j]`表示从区间(i,j)的最优解（区间DP）

区间dp的定义是在一段区间上进行动态规划，求解一段区间上的最优解。并通过合并小区间的最优解进而得出大区间上最优解的dp算法。

例题1：病毒检测

小明最近在做病毒自动检测，他发现，在某些library 的代码段的二进制表示中，如果包含子串并且恰好有k个1，就有可能有潜在的病毒。library的二进制表示可能很大，并且子串可能很多，人工分析不可能，于是他想写个程序来先算算到底有多少个子串满足条件。如果子串内容相同，但是开始或者结束位置不一样，则被认为是不同的子串。

注：子串一定是连续的。例如”010”有6个子串，分别是 “0, “1”, “0”, “01”, “10”, “010”

输入例子1:
1
1010
输出例子1:
6
说明：
满足条件的子串有："1", "1", "10", "01", "10", "010".

思路

这道题思路并不难，假设dp[i][j]是区间(i,j)中1的个数，那么dp[i][j]=dp[i][j-1]+str[j] == '1' ? 1 : 0，这样做需要的空间为n×n，从空间优化的角度考虑，我们可以将其转化为一维dp，代码如下：

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner scanner=new Scanner(System.in);
        int k=scanner.nextInt();
        scanner.nextLine();
        String s=scanner.nextLine();
        int num=0,len=s.length();
        int[] dp=new int[len];  //dp[i]表示1的数目和为i的个数
        long result=0;
        dp[0]=1;     //初始条件代表1的数目为0的
        for(char c:s.toCharArray()){
            if(c=='1') num++;    //num表示1的个数
            if(num-k>=0) result += dp[num-k];   //这一句是最难理解的，可以知道的是当num-k时不满足条件，result不更新，否则加上和为 num-k 的个数再加一遍，因为多了1个数，就会产生dp[num-k]个字串
            dp[num]++;           //如果c=='0'，那么dp[num] 必然++，因为0不影响1的个数，
            					 //如果c=='1'，那么num++后，dp[num]也要++，所以无论如何dp[num]都要++
        }
        System.out.println(result);
    }
}

`DP[i][j]`表示包含nums(i,j)的最优解（区间DP）

`dp[i][j]`表示`s1`前`i`个字符和`s2`前$j$个字符之间的关系（线性DP）

10. 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符

‘*’ 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。

思路

我们按照解决DP问题的一般思路，先明确初始状态以及DP数组的含义，然后列出状态转移表，从而找到状态转移方程，为了方便考虑，我们给定一个具体的例子，令s="aab"，p="c*a*b"并给出空的状态转移表

p/s		0	1(0)	2(0)	3(0)
		null	a	a	b
0	null	T	F	F	F
1(0)	c	F	↘F	↘F	↘F
2(1)	*	T
3(2)	a	F	↘F	↘	F
4(3)	*	T
5(4)	b	F	F	F	↘

观察上方的状态转移表，其中括号中代表字符位置，前面的数字代表字符串长度。首先考虑初始条件，dp[0][0]的含义是s前0个字符能否和p前0个字符匹配，显然是可以的，另外我们知道当s不为空而p为空时，一定不能匹配，所以第一行都是$false$。不过当s为空，p不为空时，我们不能想当然地认为无法匹配，例如dp[0][2]，s=""，而p="c*"，由于可以匹配0个或多个，如果匹配0个，此时p为空，可以匹配，所以对于dp[0][i]，如果i为 ，那么p末尾两个字符可以视为不存在，即dp[0][i] = dp[0][i-2]。所以我们得到初始化条件如下：

dp[0][0] = 1; 
for(int i = 1;i<=n;i++){
    if(p[i-1] == '*') dp[0][i] = dp[0][i-2];
}

现在我们考虑对.和一般字符进行匹配的情况，这个比较简单，如果s[i] == p[j] || p[j] == .那说明这个字符是匹配的，我们只需要看前i-1和前j-1个字符是否匹配即可，转移方程如下：

$dp[i][j]=dp[i-1][j-1] \ \ \ \ if:\ \ p[j] == '.'\ \ or\ \ ischar(p[j]) \ \ and\ \ s[i]=p[j]$

如果两个字符不匹配，那肯定就是$false$。这样我们的表格中凡是字母或.与字母进行匹配的都可以进行填充，表格中的箭头表示了状态转移的方向。没有填充的是目前还不知道的。接下来我们考虑最麻烦的，当p[j]=*的情况。该情况又可以分为两种子情况：

*号匹配0个字符串，此时意味着将p最后两个字符直接抛弃，那么dp[i][j] = dp[i][j-2]
号匹配多个字符串，此时我们要先将s[i]和\之前的字符进行比较，如果两个字符相同，那么意味着这个字符可以删掉，我们只需要看s抹去第i个字符后和p是否相同即可，这里需要理解一下，因为通配符并不占用实际字符，因此此时是s[0,...,i-1]和p[0,...,j]进行比较

我们举一个具体的例子，s="acdee"，p="acde*"，i=4,j=4可以看到s[i]=p[j-1]，我们抹掉s[i]，而s="acde"和p匹配，所以结果为true，经过上面的过程，我们得到状态转移方程如下：

$dp[i][j]= dp[i][j-2]\ ||\ dp[i-1][j]$

这里引出了最后一个问题，我们知道当*前的字符和s[i]相同时，我们可以匹配0个或多个，但是当字符不同呢，那我们就将p[j]和p[j-1]抛弃，至此我们完全地写出了状态转移的方程：

for(int i = 1;i<=s.size();i++){
    for(int j=1;j <= p.size(); j++){
        if(s[i-1] == p[j-1] || p[j-1] == '.') dp[i][j] = dp[i-1][j-1];   
        else if(p[j-1] == '*'){
            if(p[j-2] == s[i-1] || p[j-2] == '.') dp[i][j] = dp[i][j-2] || dp[i-1][j];
            else dp[i][j] = dp[i][j-2];
        }
    }
}

相似问题还有44. 通配符匹配

状态转移方程

`dp[i][j]`和`dp[i-1][j]`、`dp[i][j-1]`或者`dp[i-1][j-1]`有关

这种情况算是二维dp中比较常见的情况，相关例题如下：

72. 编辑距离

规划方向（自上而下还是自下而上）

动态规划有两种等价实现方法，带备忘录的自顶向下和自底向上方法。

一般来说，动态规划我们采用自上而下的方式，以迷宫题为例，一般是从起点开始，向终点搜索。而在有些情况下，使用自下而上的方式可能会令编码更加简单，这里我们以一道题目为例，对自下而上和自上而下两种情况进行讨论。

120. 三角形最小路径和

自上而下的解法

自上而下的解法很直观，dp[i][j]表示包含triangle[i][j]的最优解，这里直接给出代码：

class Solution {
    public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int len = triangle.size();
        if (len == 0) return 0;

        int dp[len][len];
        dp[0][0] = triangle[0][0];

        for (int i = 1; i < len; i++) {
            int n =  triangle[i].size();
            for (int j = 0; j < n; j++) {
                if (j == 0) {
                    dp[i][j] = dp[i - 1][j] + triangle[i][j];
                }  else if (j == n - 1){
                    dp[i][j] = dp[i - 1][j - 1] + triangle[i][j];
                } else {
                    dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1]) + triangle[i][j];
                }
            }
        }

        int ans = INT_MAX;
        for (int i = 0; i < len; i++) {
            if (ans > dp[len - 1][i]) ans = dp[len - 1][i];
        }
        return ans;
    }
};

自下而上的解法

自下而上的思想和深度优先搜索类似，都是先找到解空间中的叶子节点，然后自下而上逐步求解，有些情况下，自下而上的解法比自上而下的要简单许多。

class Solution {
    public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int len = triangle.size();
        if (len == 0) return 0;

        for (int i = len - 2; i >= 0; --i) {
            for (int j = 0; j < triangle[i].size(); ++j) {
                triangle[i][j] += min(triangle[i + 1][j], triangle[i + 1][ j + 1]); //自下而上搜索解空间
            }
        }
        return triangle[0][0];
    }
};

状态转移表

要写好动态规划，我们要尽可能列举出状态转移表，通过状态转移表能够清晰地分析出状态转移的过程，从而列举出正确的状态转移方程。

边界处理

由于动态规划涉及旧值处理，因此状态转移方程中可能会包含边界溢出的情况，例如下列的状态转移方程：

dp[i]=dp[i-1]+dp[i-2]，当i==1时，dp[i-2] == dp[-1]，发生了溢出。若单独判断i==1，程序又会变得更加繁琐，因此我们可以添加类似于哑节点的初始条件，从而避免边界位置的特殊判断，比如我们可以令dp[-1] == 0 或 1，具体的值需要根据问题确定。

91. 解码方法

动态规划算法优化

降维

当我们使用二维动态规划时，可以考虑将其进行压缩，将二维降低为一维，从而降低空间复杂度。我们以一道例题为例，讲解动态规划的降维过程。

剑指 Offer 47. 礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

例子：

1 10 3 8

12 2 9 6

5 7 4 11

3 7 16 5

思路

如果我们使用二维动态规划，状态转移方程为$f(i,j)=\max(f(i-1,j)+f(i,j-1))+max_value(i,j)$。从公式中我们可以看出，礼物的最大价值只依赖坐标$(i-1,j)$和$(i,j-1)$，而第$i-2$行和更上面的格子其实没有必要保存。从这个角度，我们可以进行压缩。每次只记录最新的结果，之前的就都抛弃掉，只使用一维数组即可保存中间结果。

传统的二维动态规划

礼物的最大价值表	1	2	3	4
1	1	11	14	22
2	13	15	24	30
3	18	25	29	41
4	21	32	48	53

如果我们只保存一行（或一列），那么二维就转为了一维。

礼物的最大价值表	1	2	3	4
旧行	13	15	24	30
新行	13+5	$\max(13+5, 15)+4$	24

代码

int getMaxValue(const int* values, int rows, int cols){
    if(values == nullptr || rows <= 0 || cols<=0) return 0;
    
    int *max_value = new int[cols];
    for(int i=0;i<rows;++i){
        for(int j=0;j<cols;++j){
            int left = 0;
            int up   = 0;
            if(i>0) up   = max_value[j];     //实际上是max_value[i-1][j]，此时在新一行，max_value还未更新
            if(j>0) left = max_value[j-1];   //实际上是max_value[i][j-1];即左边的最大值 
        	max_value[j] = max(left,up) + values[i*cols+1];   //max_value[i][j]
        }
    }
    int result = max_value[cols-1];
    delete[] max_value;
    return result;
}

专题：递归改动态规划

绝大多数递归问题都可以用动态规划重写，由于动态规划在时间上具有一定优势，因此掌握递归改写动态规划是有必要的。本节将针对一些递归问题进行动态规划的改写，这些递归问题往往需要用到DFS或回溯法进行解决。一般这种场景在链表或二叉树应用中比较多一些。

例题

95. 不同的二叉搜索树 II

给定一个整数 n，生成所有由 1 … n 为节点所组成的二叉搜索树

思路1：递归

确定搜索范围

我们从序列 1 ..n 中取出数字 i，作为当前树的树根。于是，剩余i - 1 个元素可用于左子树，n - i 个元素用于右子树。这样会产生 G(i - 1) 种左子树和 G(n - i) 种右子树，其中 G 是卡特兰数。

图片名称

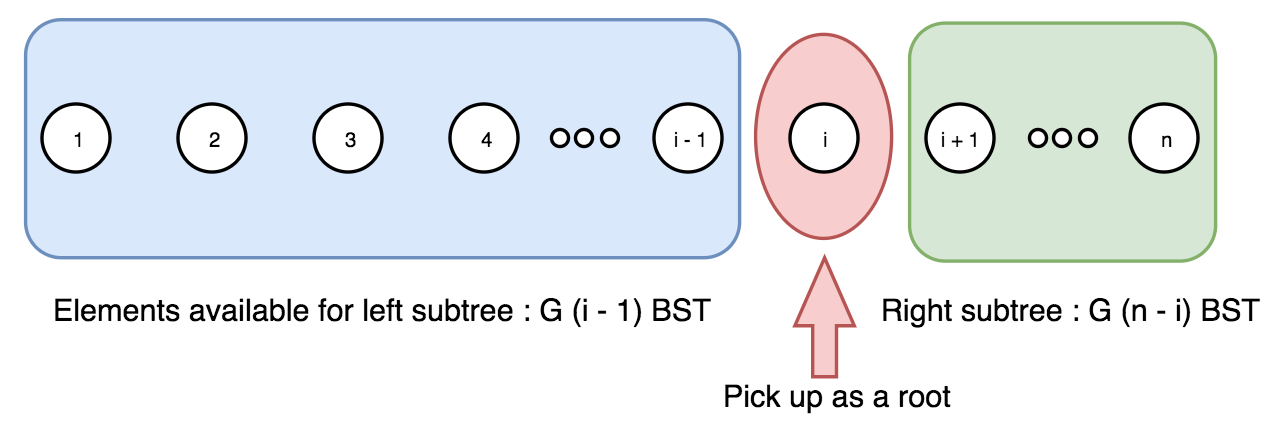
思路2：动态规划

确定搜索范围

有$n$个节点需要插入，因此需要从$1$遍历到$n$，时间复杂度为$O(n)$。同时由于每插入一个节点，当前解向量都需要更新，因此创建新的解向量用于保存插入节点的临时解（动态规划）

1
2
3

for(int i=1;i<=n;i++){
    vector<string> cur{};
}

利用之前的解向量构造新的解向量

为了利用到动态规划的思想，我们需要保存插入之前的结果，并不断更新迭代，基本思路如下：

//插入第一个节点
1
    
//插入第二个节点，在上一步插入操作的基础上进行
1              2
 \           /
  2         1

我们需要遍历之前解向量中所有的结果，针对每一个结果进行操作

for(int i=1;i<=n;i++){
    vector<string> cur{};
    for (auto root : pre){
    	...//执行插入操作
    }
    pre = cur;  //迭代更新
}

代码

问题举例

背包问题

背包问题是动态规划最经典的应用，根据物品可以被拿取的次数限制，背包问题可以分为九种：

1、0-1 背包问题：每种物品只能拿1次；

2、完全背包问题：物品可拿无限次（LeetCode 518）；

3、多重背包问题：对每一种物品可以拿的个数有限制；

4、混合背包问题：中和以上 33 种情况，有的物品只可以取一次，有的物品可以取无限次，有的物品可以取的次数有一个上限；

5、二维费用背包问题：对于每件物品，具有两种不同的费用；选择这件物品必须同时付出这两种代价；对于每种代价都有一个可付出的最大值（背包容量）。问怎样选择物品可以得到最大的价值。

6、分组背包问题：物品被划分为若干组，每组中的物品互相冲突，最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

7、有依赖的背包问题：这种背包问题的物品间存在某种“依赖”的关系。也就是说，i 依赖于 j，表示若选物品 i，则必须选物品 j。

8、泛化物品：考虑这样一种物品，它并没有固定的费用和价值，而是它的价值随着你分配给它的费用而变化。这就是泛化物品的概念。

9、输出背包问题的解决方案。²

完全背包问题

LeetCode 518 零钱兑换

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

题解：

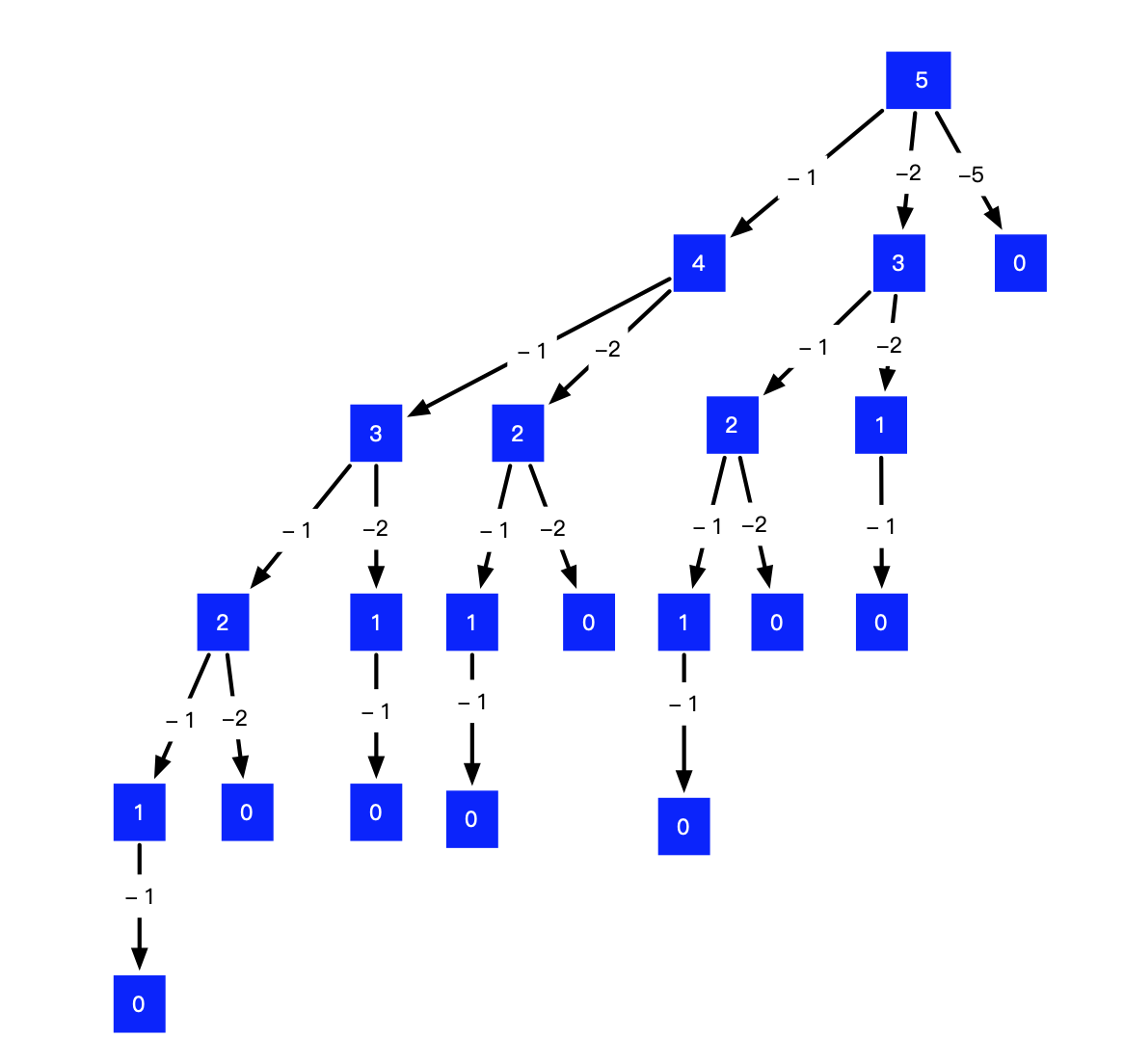
首先根据可能的情况画出分支树，里面有些路径是重复的，需要进行减枝处理，我们要保证更深层的减去的数小于或等于更浅层的数，因此剪去的枝叶如下图红色部分：

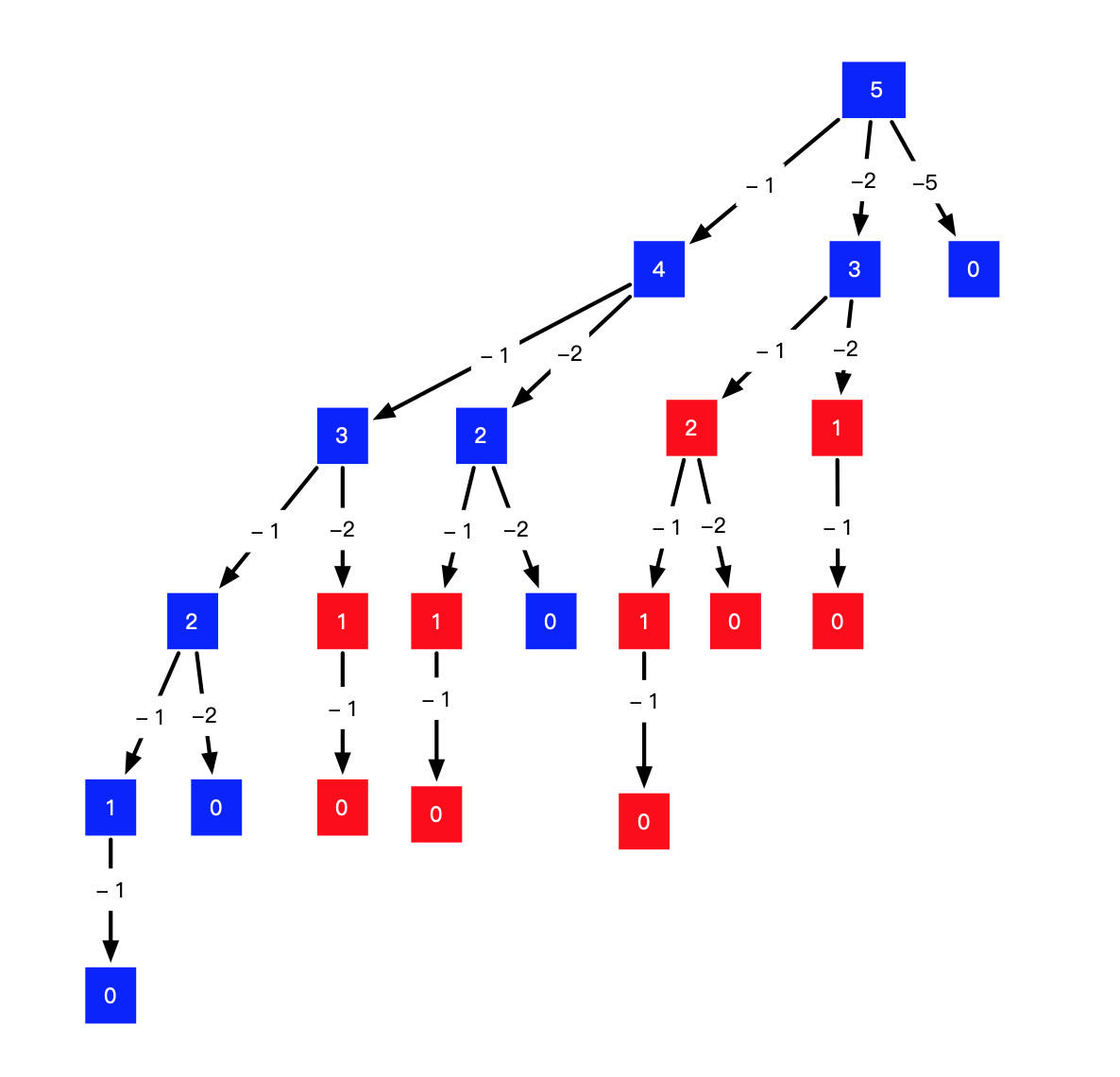
使用回溯法是可以的，但是效率太低了，这里给出几种方法：

根据状态转移方程逐行填写表格

a. 状态的定义：dp[i][j]：考虑前 i 个硬币能够凑成总金额 j 的组合数。

注意：这里的关键词是“前 i个硬币”，即考虑数组 coins 的区间范围是 [0, i - 1]，例如 dp[3][j] 考虑的是前 2 枚硬币能够凑成总金额j的组合数，考虑虑数组 coins的区间范围是 [0, 2]。

b. 填写状态转移方程

对于看到的一种面值的硬币，逐个考虑添加到“总金额”中。又由于硬币的个数可以无限选取，因此：

对于一种新的面值的硬币 coins[i - 1]（注意这里有一个位移偏差），我们可以依次考虑选取 0 枚、1 枚、2 枚，以此类推，直到选取这种面值的硬币的总金额超过“需要的总金额 j”，dp[i][j] 是它们的值的和。状态转移方程是：

dp[i][j] = dp[i - 1][j - 0 * coins[i - 1]] + 
           dp[i - 1][j - 1 * coins[i - 1]] +
           dp[i - 1][j - 2 * coins[i - 1]] + 
           ... + 
           dp[i - 1][j - k * coins[i - 1]]

这里 j - k * coins[i - 1] >= 0，即总金额必须大于或等于0。

说明：dp[i][j] 相对于dp[i - 1][j] 而言，多考虑的一枚硬币，即“最近看到的那枚硬币”，coins[i - 1]，而这枚硬币选取的个数（从 0 开始）就是 dp[i][j]这个问题可以分解的各个子问题的分类标准。

下面我们以示例输入: amount = 5, coins = [1, 2, 5] 为例，通过“打表格”的方法模拟程序是如何执行的：

初始的时候，表格如下，行表示从 0 种面值的硬币开始，依次把数组 coins 中的硬币面值考虑进来（注意这里和 0-1 背包问题的区别）。而列也是从总金额为 0 开始，依次计算凑齐总金额为 amount的组合数。

	0	1	2	3	4	5
0	1	0	0	0	0	0
1	1	1	1	1	1	1
2	1	1	2	2	3	3
3	1	1	2	2	3	4

下面用递归的形式解决背包问题：

考虑如下问题：给定一个整数N，N可以表示为1、3、4的和，问共有多少种表示方式？

例如N=5，那么答案为共6种表示方式：

1+1+1+1+1
1+4
4+1
1+1+3
1+3+1
3+1+1

子问题：令$DP_{n}$表示对于给定整数N，可能的表示方式的个数。

找递归状态转移方程：考虑一个可能的解：$n=x1+x_2+…+x_k$，如果$x_k=1$，那么剩余的部分之和为$n-1$，可能的表示方式个数为$DP{n-1}$。考虑$x_k=3$和$4$的情况，最终我们可以得到下式，这个叫做状态转移方程：

$DP_{n}=DP_{n-1}+DP_{n-3}+DP_{n-4}$

递归的基本条件：

从上面的式子我们可以看出，它不能表示$n=0,1,2,3$的情况，所以$n=0,1,2,3$是解空间的基础解系。

$DP_0=0,DP_1=1,DP_2=1,DP_3=2$

写成代码的形式：

DP[0] = DP[1] = DP[2] = 1; DP[3] = 2;
for (i = 4; i <= n; i++) {
    DP[i] = DP[i-1] + DP[i-3] + DP[i-4];
}

可以看到，解决DP问题很关键的一个步骤是：找到状态转移方程。

0-1背包问题

给定$n$个重量为$w_1, w_2,…,w_n$，价值分别为$v_1,v_2,…,v_n$的物品与容量为$C$的包，每个物品只能使用一次，求包内最大总价值。这种问题叫做0-1背包问题。0-1背包问题非常重要，是所有背包问题的基础，因此有必要完全掌握。

思路

考虑将前$i$件物品放入容量为$j$的背包中这个子问题，若只考虑第$i$件物品的策略（放或不放），那么就可以转化为一个只和前$i-1$件物品有关的问题，令$f(i,j)$表示将前$i$个物品放到容量为$j$的背包中得到的最大结果，两种选择如下：

放第$i$个物品：$f(i,j) = f(i-1,j)$
不放第$i$个物品：$f(i,j)=v_i+f(i-1,j-w_i)$

如果不放第$i$件物品，那么问题转换为“前$i-1$件物品放入背包得到的最大价值；如果放第$i$个物品，那么问题就转化为“前$i−1$件物品放入剩下的容量为$j-w_i$的背包中”，此时能获得的最大价值就是$f(i-1,j-w_i)$再加上通过放入第$i$件物品获得的价值$v_i$。

优化

以上方法时间与空间复杂度均为$O(nC)$，我们可以针对空间复杂度进行优化，使空间复杂度降为$O(n)$。首先我们观察二维$dp$的实现，$dp[i][j] = f(i,j)$，我们首先需要一个主循环$i=1…n$，从而计算$dp[i][1…C]$所有值。如果要改改成1维dp，那么我们希望$dp[j]$代表对于前$i$个物品空间为$j$所能拿取的最大价值，再套上一个循环$i=1…n$，我们就可以在每次循环中更新$dp[j]$，从而令$dp[j]=dp[i][j]$，我们的递推公式变为：

$f(j)=max(f(j), v_i+f(j-w_i))$

其中，左侧$f(j)$为更新后的值，即考虑前$i$个物品的$f(j)$，即$f(i,j)$，右侧为更新前的值，为$f(i-1,j)$，代码如下：

代码

1
2
3

for (int i = 1; i <= n; i++)
    for (int j = C; j >= w[i]; j--)   //从最大容量开始考虑，一直考虑到最小容量即w[i]
        dp[j] = max(dp[j], dp[j - w[i]] + v[i]);

内层循环为何逆序

上面的代码需要注意的一点是$j$是递减的，因为如果是正序遍历，当求$f(j)$时，$f(0),f(1),…,f(j-1)$可能已经发生了变化，即$f(i,0),…,f(i,j-1)$而非$f(i-1,0),…,f(i-1,j)$，因此我们必须逆序，因为计算$f(j-1)$不需要用到$f(j)$，但是计算$f(j)$会用到$f(j-1)$。我们必须保证没有发生脏读的情况。

题目

1049. 最后一块石头的重量 II

有一堆石头，每块石头的重量都是正整数。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；

如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

思路

这个问题可以转换为0-1背包问题，设石头总重量为$W$，那么我们需要选出最接近$W/2$的石头，就是将石头尽可能均分为两堆，这样粉碎的石头重量是最多的。问题就转换为了求0-1背包最大价值，最大容量为$W/2$

最长公共子序列问题（Longest Common Subsequence，简称 LCS）

给出两个数组，求最长的公共子序列(LeetCode1143)以及1035. 不相交的线

输入: str1 = “abcde”, str2 = “ace”
输出: 3
解释: 最长公共子序列是 “ace”，它的长度是 3

注意，子序列必须保证是递增的，例如’aec’不能称为str1或str2的子序列

int longestCommonSubsequence(string text1, string text2) {
    int m = text1.size();
    int n = text2.size();
    vector<vector<int>> dp(m+1,vector<int>(n+1,0)); //dp[i][j]代表text1[0...i-1]和text2[0...j-1]两个字串的最长公共子序列
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(text1[i] == text2[j]) dp[i+1][j+1] = dp[i][j]+1;  //新加入的字符为公共字符，那么公共子序列长度加1
            else{
                dp[i+1][j+1] = max(dp[i][j+1],dp[i+1][j]);
            }
        }
    }
    return dp[m][n];
}

数列连续和或区间和问题（前缀和）

面试题 16.17. 连续数列

给定一个整数数组（有正数有负数），找出总和最大的连续数列，并返回总和。

输入： [-2,1,-3,4,-1,2,1,-5,4]
输出： 6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6。

int maxSubArray(vector<int>& nums) {
    if(nums.empty()) return INT_MIN;
    int max_subarray = nums[0];
    for(int i=1;i<nums.size();++i){
        if(nums[i-1] >= 0){
            nums[i] = nums[i-1] + nums[i];
        }
        max_subarray = max(max_subarray,nums[i]);
    }
    return max_subarray;
}

令dp[i]表示以i为结尾的最大连续数列，那么dp[i]的状态转移方程如下：

如果dp[i-1]小于0，那么dp[i] = nums[i]，因为dp[i-1]对dp[i]的增长起副作用
如果dp[i-1]大于0，那么dp[i]=dp[i-1]+nums[i]，此时dp[i-1]对dp[i]的增长起正作用。

前缀和问题

对于一个数组A，其前缀和的定义为A[0]+A[1]+A[2]+…+A[i]，即

$presum[i]=\sum_{j=0}^{i}A[j]$

在实际使用中，出于方便角度考虑，定义一个辅助位，令preSum[0] = 0，preSum[1] = 0 + A[1]，这样计算起来比较方便。

例题

304. 二维区域和检索 - 矩阵不可变

数列连续积或区间积问题

与区间连续和类似，区间连续积要求区间乘积的最大或最小值。和区间连续和不同的是，由于负数的存在，所以有可能两个负数的乘积会变成一个正数而影响结果，我们以LeetCode152. 乘积最大子数组为例，对该问题进行解决。

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字）。

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

我们不仅要考虑最大值，还要考虑最小值，当出现负数时，最大值乘负数变为了最小值，而最小值乘负数变成了最大值。因此我们需要两个变量记录最大值与最小值，并在出现负数的时候将最大值与最小值进行交换。

求组合问题

LeetCode 552 学生出勤记录

给定一个正整数 n，返回长度为 n 的所有可被视为可奖励的出勤记录的数量。答案可能非常大，你只需返回结果mod $10^9 + 7$的值。

学生出勤记录是只包含以下三个字符的字符串：

‘A’ : Absent，缺勤
‘L’ : Late，迟到
‘P’ : Present，到场
如果记录不包含多于一个’A’（缺勤）或超过两个连续的’L’（迟到），则该记录被视为可奖励的。

一看到求组合，就知道是典型的动态规划，解决问题从两个点着手，传递函数和基本例。思路如下：

首先简化问题，我们将问题分为包括A与不包括A两种，先解决不包括A，再分析包括A怎么做。

不包括A

在不包括A的情况下，又可以分为两种
- 结尾为P，即第i天为P，那么dp[i] = dp[i-1]
- 结尾为L，第i天为L，此时需要进一步讨论
  - 若结尾为PL（LPL及PPL），那么dp[i] = dp[i-2]
  - 若结尾为PLL，那么dp[i] = dp[i-3]
  - 结尾不能为LLL
这样算下来我们的递推公式就有了dp[i] = dp[i-1]+dp[i-2]+dp[i-3]
包括A

在包括A的情况下，我们只需要考虑A在哪一天，假设A在第i天，那么我们的出勤表为：
$[1,2,...,i-1], A ,[i+1,i+2,...,n]$
可以看到不断调整A的位置，我们就可以得到所有的情况，若A在第i天，则dp[n]要加上dp[i-1]*dp[n-i]

LeetCode903 DI序列的有效排列

我们给出S，一个源于{'D', 'I'} 的长度为 $n$ 的字符串。（这些字母代表 “减少” 和 “增加”。）
有效排列是对整数$ {0, 1, …, n} $的一个排列$ P[0], P[1], …, P[n]$，使得对所有的 i：

如果 S[i] == 'D'，那么 P[i] > P[i+1]，以及；
如果 S[i] == 'I'，那么 P[i] < P[i+1]。
有多少个有效排列？因为答案可能很大，所以请返回你的答案模 10^9 + 7.

输入："DID"
输出：5
解释：
(0, 1, 2, 3) 的五个有效排列是：
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)

一开始的一个很朴素的解决方法就是先求出全排列，然后依次排除不符合的答案，最后统计个数，然后不出意外的超时了，想用动态规划，但是没有找到合适的递归函数，因此参考下下面的答案：

一开始的时候，我尝试使用1维dp数组解决问题，但是我发现了一个问题，即我找不到dp[i]与dp[i-1]之间有什么关系，而答案中的解法采用了一个二维dp数组，dp数组的每一个维度，实际上就是一个约束条件，dp[i][j]定义如下：

dp[i][j]表示前i+1个数字的可能排列，其中第i+1个数字是剩余数字中的第j+1小的数，说起来可能不是很好理解，看下面的图片：

看dp[0][3]，第一位数字，并且在剩余的数字（1,2,3,4）中是第四小，那就是4，在确定了4之后，如果我们的S[0]是D，那么我只能在剩余数字中第1、2、3小中寻找下一位，如果S[0]是I，那么我只能在第4位向上寻找下一位（找不到了），因此我们就找到了dp中的递推关系。

int numPermsDISequence(string S) {
    int n = S.length(), mod = 1e9 + 7;
    vector<vector<int>> dp(n + 1, vector<int>(n + 1));
    for (int j = 0; j <= n; j++) dp[0][j] = 1;     //初始化
    for (int i = 0; i < n; i++)
        if (S[i] == 'I')  //递增，向上累加
            for (int j = 0, cur = 0; j < n - i; j++) //只能在第1到第n-i+1个大的数中进行寻找
                dp[i + 1][j] = cur = (cur + dp[i][j]) % mod;
    	else  //递减，向下累加
        	for (int j = n - i - 1, cur = 0; j >= 0; j--)  //只能在第
          	 	dp[i + 1][j] = cur = (cur + dp[i][j + 1]) % mod;
    return dp[n][0];
}

求解概率问题

这里以一道简单的DP算法求解概率的问题为例，总结下此类问题的解决方式。

Two friends Kunal and Satyam are playing an interesting game. They take turns drawing a ball from a bag which initially contains R red balls and G green balls. Each player draws a ball alternatively and never put it back. The person who is the first to draw a red balls wins. Satyam always draws first. If there are no more balls in the bag and nobody has drawn a red ball, the satyam wins.

What is the probability of the Satyam winning?
Input:
The first line will contain the number of test cases T.
The first line of each test case will contain a number R (number of red balls) and G(number of green balls )

Output
For each testcase, print the desired probability.
Constraints:
1<=T<=10
0<=R,G<=10^3¹

子问题：我们用$r,g$分别代表红球和绿球的个数，那么$DP_{rg}$代表该情况下Satyam获胜的概率。

找递归状态转移方程：

考虑如下情况：

如果Satyam抽出的是红球，那么游戏结束，在这种情况下$DP_{rg}=r/(r+g)$。
如果抽出的是绿球，那么轮到Kunal抽球，Kunal抽到红球的情况下游戏结束，而抽到绿球游戏才会继续，在这种情况下$DP{rg}=g/(r+g)×(g-1)/(r+g-1)×DP{rg-2}$。

综合考虑上面两种情况，我们最终得到

$DP_{rg}=r/(r+g)+g/(r+g)×(g-1)/(r+g-1)×DP_{rg-2}$

这个式子就后半部分比较绕一些，先是Sytyam抽到绿色球，概率是$g/(r+g)$，然后是Kunal抽到绿色，概率是$(g-1)/(r+g-1)$，最后又是在新的一轮比赛中，Sytyam抽到了红球，概率是$DP_{rg-2}$。这样我们就找到了递归的状态转移方程。

字符串问题

二维数组DP问题

求最大面积或形状的个数

221. 最大正方形

1277. 统计全为 1 的正方形子矩阵

专题：打家劫舍问题（跳跃式动态规划）

在动态规划中有一类常见问题，即由于选择的不同而出现了分支，这里对此类问题进行总结。

情况1：房屋不构成环，不能偷取相邻的房屋

198. 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

这道题目中可以看出，我们每次偷钱是有选择的，对于第i家，有两种情况，要么偷，要么不偷，由此引出了选择二叉树，解决此类问题的方法步骤如下：

首先考虑起始的分支情况，要么偷第一间房子，要么偷第二间房子，不存在第三种情况，因为如果一开始就偷第三间房子，就错过了偷第一间房子的机会。
然后根据起始分支情况列出状态转移方程，本题中情况就两种，令$f(i)$为前i个房子的最大值，那么$f(i)$只能来源于以下两种情况
- 偷第i间房子，$f(i) = f(i-2)+num[i]$
- 不偷第i间房子，$f(i) = f(i-1)$

情况2：房屋构成环

在此情况下，房屋构成了环，因此首尾相连，我们不能同时偷首尾的房子，这种情况下我们应当如何利益最大化呢？此时我们考虑首尾的情况，有以下三种：

偷首不偷尾
偷尾不偷首
首尾都不偷

易知第三种情况肯定达不到利益最大化，因此我们只需要考虑1和2谁最大即可，就转换为了问题1，分别计算偷0,～n-2号的房屋和偷1～n-1号房屋哪个钱更多即可。代码如下：

int robRange(vector<int> nums, int start, int end) {
    int n = nums.length;
    int dp_i_1 = 0, dp_i_2 = 0;
    int dp_i = 0;
    for (int i = end; i >= start; i--) {
        dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);   //从后往前，自底向上
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i;
}

专题：股票交易问题³

利润最大化问题包含多个变种，例如交易次数限制，交易包含税率或冻结期等等。本文将针对LeetCode中出现的六种股票交易问题进行总结，本文参考文献出自参考文献³。

一般例子

最一般化的股票交易问题为，给定每日股价，求最大交易利润，这个问题取决于两个方面：

我们能进行多少次交易
我们处在第几个交易日，当天股价多少

令price表示股价数组，共n天，i表示天数为第几天(从0-i-1)，k表示最大交易次数，那么我们的DP数组含义为：dp[i][k]表示在第i天最多进行k次交易取得的最大利润。基本例为：dp[-1][k] = dp[i][0] = 0，意味着没有交易日或只能进行0次交易时，获得的利润为0。现在我们考虑如何计算dp[i][k]，即寻找dp[i-1][k]、dp[i][k-1]和dp[i-1][k-1]...之间的关系。

现在，为了考虑每一天能够获得的最大利润，我们需要考虑当天进行哪些操作，我们能够进行的操作一共有三种：买入、持有、卖出，我们可以依次尝试，看哪一种能够为我们带来最大的利润。当然，我们的操作要符合实际情况，买入时手中尚无股票，卖出时手中必须有股票。这样，我们将dp再进行改进，分为dp[i][k][0]和dp[i][k][1]，分别代表第i天经过k次交易手中没有股票和有股票的最大利润，我们的基本例和状态转移方程如下：

基本例

1 2	dp[-1][k][0] = 0, dp[-1][k][1] = -Inf //初始不买入，资产为0，非法情况定义为-inf dp[i][0][0] = 0, dp[i][0][1] = -Inf

状态转移方程

1 2	dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]) //max中分别为持有和卖出 dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) //持有和买入

具体问题分析

情况1：k=1

在此情况下，我们只有两个变量，dp[i][1][0]和dp[i][1][1]，状态转移方程为：

1
2
3

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])     //max中分别为持有和卖出
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])   //持有和买入
dp[i-1][0][0] = 0

我们的代码可以写为：

int maxProfit(vector<int>& prices) {
    int dp_i10 = 0, dp_i11 = INT_MIN;

    for(int i=0;i<prices.size();i++){
        dp_i10 = max(dp_i10, dp_i11 + prices[i]);
        dp_i11 = max(dp_i11, -prices[i]);
    }
    return dp_i10;
}

情况2：k无限，包含手续费

在此情况下，我们可以无限次进行交易，此时我们的变量为dp[i][k][0]和dp[i][k][1]，状态转移方程如下：

1 2	dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + price[i]-fee) //fee为卖出时的手续费 dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - price[i])

表面上看我们需要5个变量，但实际上由于k=Inf，所以dp[][k-1][]=dp[][k][](一点极限的思想)，因此我们可以减少变量的个数，代码如下所示：

dp[0][0] = 0
dp[0][1] = INT_MIN

//转移方程
old_dpi0 = dpi0
dpi0 = max(dpi0, dpi1 + price[i])
dpi1 = max(dpi1, old_dpi0 - price[i])

情况3：k为任意值

在此情况下，我们有交易次数限制，此时我们需要对交易次数进行统计，当达到最大交易次数后，返回最大值。此时我们需要分类讨论

当k >= prices.size()时，此时可以退化为情况2
当k < prices.size()时，此时需要三维dp，递推公式如下：

1 2	dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + price[i]) dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - price[i])

我们的代码如下：

public int maxProfit(int k, int[] prices) {
    //当k过大会导致内存溢出，因此先对case2进行判断
    if (k >= prices.length >>> 1) {
        int T_ik0 = 0, T_ik1 = Integer.MIN_VALUE;
    
        for (int price : prices) {
            int T_ik0_old = T_ik0;
            T_ik0 = Math.max(T_ik0, T_ik1 + price);
            T_ik1 = Math.max(T_ik1, T_ik0_old - price);
        }
        
        return T_ik0;
    }
        
    int[] T_ik0 = new int[k + 1];
    int[] T_ik1 = new int[k + 1];
    Arrays.fill(T_ik1, Integer.MIN_VALUE);
        
    for (int price : prices) {
        for (int j = k; j > 0; j--) {
            T_ik0[j] = Math.max(T_ik0[j], T_ik1[j] + price);
            T_ik1[j] = Math.max(T_ik1[j], T_ik0[j - 1] - price);
        }
    }
        
    return T_ik0[k];
}

情况4：k无限，但是有交易冷却

交易冷却会限制我们的交易频次，当我们在卖出股票后，无法在第二天买入，冷冻期为1天

1 2	dp[i][0] = max(dp[i-1][0], dp[i-1][1] + price[i]) dp[i][1] = max(dp[i-1][1], dp[i-2][0] - price[i])

因此我们在计算过程中，需要保存前天的股票交易情况。

什么是动态规划？

动态规划解决什么问题？

动态优化框架

算法优缺点

DP延伸算法

状态压缩DP

数位DP

DP难点总结

一维DP

DP[i]的含义

DP[i]代表以vec[i]为结尾的某种状态

DP[i]就代表第i个要求的解

状态转移方程

dp[i]的状态转移方程和前i个状态(dp[0] ~ dp[i-1])均可能有关

dp[i]和前某几个状态有关

二维DP

DP[i]的含义

DP[i][j]表示条件为i，结果为j时的次数或最优解

DP[i][j]表示从区间(i,j)的最优解（区间DP）

DP[i][j]表示包含nums(i,j)的最优解（区间DP）

dp[i][j]表示s1前i个字符和s2前$j$个字符之间的关系（线性DP）

状态转移方程

dp[i][j]和dp[i-1][j]、dp[i][j-1]或者dp[i-1][j-1]有关

规划方向（自上而下还是自下而上）

状态转移表

边界处理

动态规划算法优化

降维

剑指 Offer 47. 礼物的最大价值

专题：递归改动态规划

例题

95. 不同的二叉搜索树 II

思路1：递归

思路2：动态规划

代码

问题举例

背包问题

完全背包问题

0-1背包问题

题目

最长公共子序列问题（Longest Common Subsequence，简称 LCS）

数列连续和或区间和问题（前缀和）

前缀和问题

例题

数列连续积或区间积问题

求组合问题

求解概率问题

字符串问题

二维数组DP问题

求最大面积或形状的个数

专题：打家劫舍问题（跳跃式动态规划）

情况1：房屋不构成环，不能偷取相邻的房屋

情况2：房屋构成环

专题：股票交易问题3

一般例子

具体问题分析

情况1：k=1

情况2：k无限，包含手续费

情况3：k为任意值

情况4：k无限，但是有交易冷却

参考文献

`DP[i][j]`表示条件为i，结果为j时的次数或最优解

`DP[i][j]`表示从区间(i,j)的最优解（区间DP）

`DP[i][j]`表示包含nums(i,j)的最优解（区间DP）

`dp[i][j]`表示`s1`前`i`个字符和`s2`前$j$个字符之间的关系（线性DP）

`dp[i][j]`和`dp[i-1][j]`、`dp[i][j-1]`或者`dp[i-1][j-1]`有关

专题：股票交易问题³