状态机在处理一些比较复杂的状态转移问题时往往非常有用。它能够较为清晰地列举出每种状态之间的关系,当给定某个输入时,能够给出输出的状态,本文将对状态机的知识及使用场景进行总结。
状态机定义及分类
状态机由状态寄存器和组合逻辑电路构成,能够根据控制信号按照预先设定的状态进行状态转移,是协调相关信号动作、完成特定操作的控制中心。有限状态机简写为FSM(Finite State Machine),主要分为2大类:
Moore机:若输出只和状态有关而与输入无关
Mealy状态机:输出不仅和状态有关而且和输入有关系
在算法中,状态机是一个有向图形,由一组节点和一组相应的转移函数组成。状态机通过响应一系列事件而“运行”。每个事件都在属于“当前” 节点的转移函数的控制范围内,其中函数的范围是节点的一个子集。函数返回“下一个”(也许是同一个)节点。这些节点中至少有一个必须是终态。当到达终态, 状态机停止。
状态机的组成
- 状态集(states)
- 一个起始状态(start state)
- 一组输入符号集(alphabet)
- 一个映射输入符号
- 当前状态到下一状态的转换函数(transition function)的计算模型
状态机的使用步骤
本节将对状态机使用步骤进行总结,具体使用案例参考本文状态机应用章节。
考虑所有可能的状态和状态转移方程
我们将初始状态设为状态0,非法状态设为-1,然后根据状态转移方程,可以获得中间状态。
列出状态转移图
状态机最关键的一个步骤就是列出状态转移图。首先由初始态开始,然后根据不同的状态转移方程,列举出状态转移图
列出状态转移表
根据状态转移图,列出状态转移表,其中行表示不同的状态,列表示状态转移方程。
列出有效状态
在所有状态中,筛选出符合条件的状态,并保存至一个集合中
根据状态表和有效状态,编写程序
状态机应用
判断某个字符串是否合法
LeetCode 面试题20. 表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串”+100”、”5e2”、”-123”、”3.1416”、”0123”及”-1E-16”都表示数值,但”12e”、”1a3.14”、”1.2.3”、”+-5”及”12e+5.4”都不是。
思路
设置初始状态为状态0,那么字符串中共有6个状态转移方程,分别是数字、小数点、+-号,指数标志e或E、空格、其他字符。
根据状态转移方程,获得中间状态并绘制状态转移图
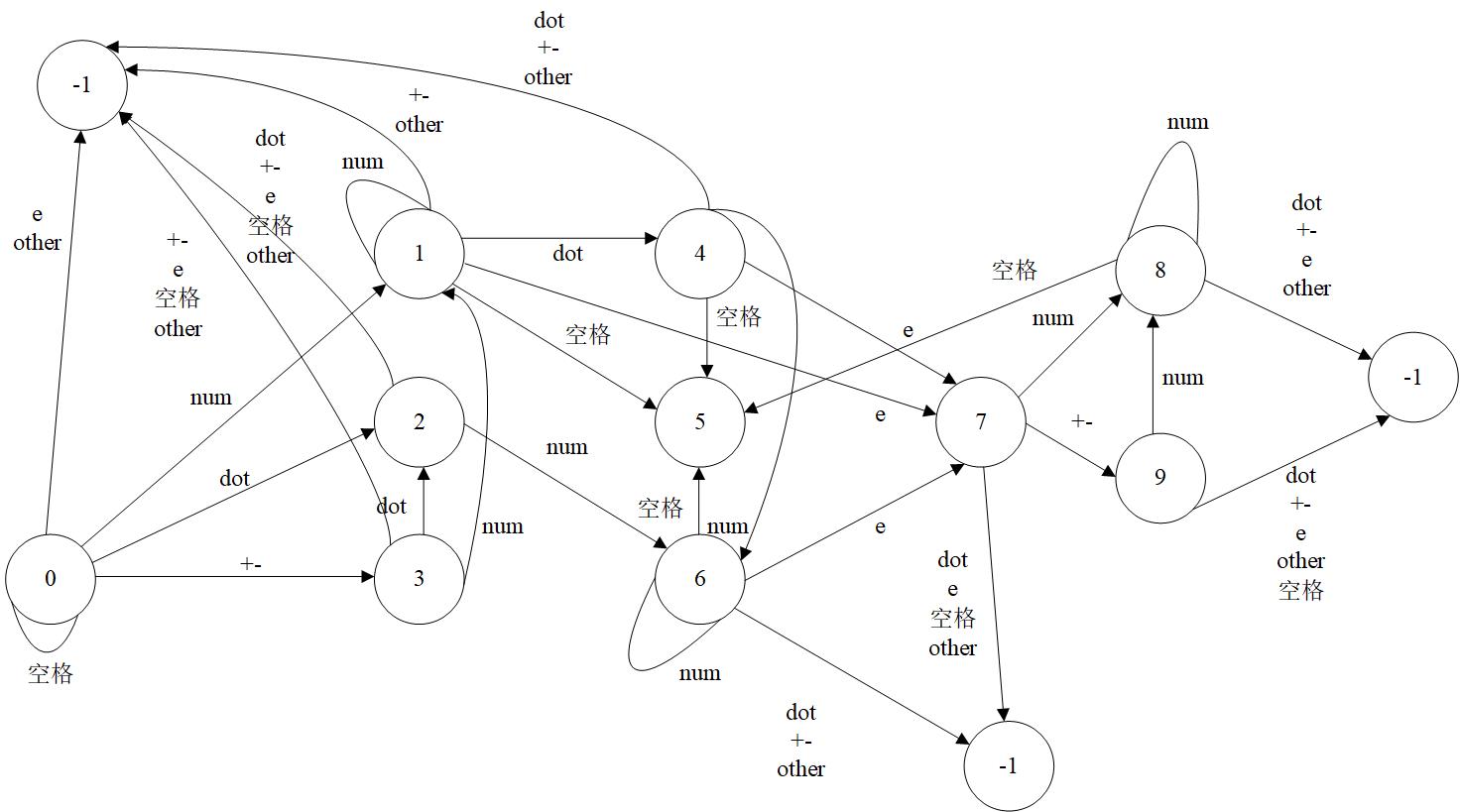
- 根据状态转移图列出状态转移方程
| num | dot | +- | e | 空格 | other | |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | -1 | 0 | -1 |
| 1 | 1 | 4 | -1 | 7 | 5 | -1 |
| 2 | 6 | -1 | -1 | -1 | -1 | -1 |
| 3 | 1 | 2 | -1 | -1 | -1 | -1 |
| 4 | 6 | -1 | -1 | 7 | 5 | -1 |
| 5 | -1 | -1 | -1 | -1 | 5 | -1 |
| 6 | 6 | -1 | -1 | 7 | 5 | -1 |
| 7 | 8 | -1 | 9 | -1 | -1 | -1 |
| 8 | 8 | -1 | -1 | -1 | 5 | -1 |
| 9 | 8 | -1 | -1 | -1 | -1 | -1 |
- 列出有效状态
legal_state = {1,4,5,6,8}
完整代码如下:
1 | class Solution { |