“The great wall is made by blocks”
布尔函数基础
计算机组成原理课程的第一周1,本周我们将使用HDL搭建基本门电路,构建起组成CPU的基本单元。首先记住德摩根定律
根据真值表就能得到上面的规律,下面我们讨论布尔函数与真值表之间的转换。根据布尔函数能够很容易推出真值表,那么如何根据真值表反推布尔函数呢?例如给定如下真值表:
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
如何根据上述真值表推出如下函数:
方法如下:
- 遍历真值表中$f(x,y,z)=1$的行
- 用与逻辑表示等式,例如$f(0,0,1)=1$可以表示为:$\neg (x)\and \neg(y) \and z = 1$,可以证明该等式仅在当前行生效,将所有为1的行相加,我们得到真值表对应等式为:
- 将上面的公式进行化简,得到$f(x,y,z)=(x\and y)\or(\neg x\and z)$,化简过程实际上是一个很难的问题,但是这里我们得到了第一个结论
$\textrm{Theory}\ 1$: 所有的布尔函数都可以用简单的与、或、非来表示,进一步地,根据德摩根定律,$(x\or y)=\neg (\neg x\and \neg y)$,所以所有的布尔函数都可以用简单的与、非来表示
为了进一步化简,我们引入NAND($\neg (x\and y)$),真值表如下:
| x | y | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
实际上,NAND(x,x)即为$\neg x$,我们可以将Theory 1进一步化简,所有布尔函数都可以用NAND简单表示,证明如下:
所以这个世界实际上是NAND(与非门)组成的。
逻辑门与HDL
基本逻辑门
我们现在来讨论如何用硬件实现布尔逻辑,由于我们知道这个世界是由NAND组成的,我们来讨论如何构造一个NAND门
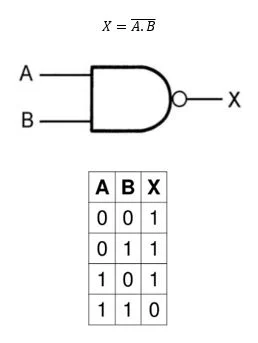
用代码描述得到与非门如下:
1 | bool NAND(bool x, bool y){ |
总结下常见的门和对应的真值表:
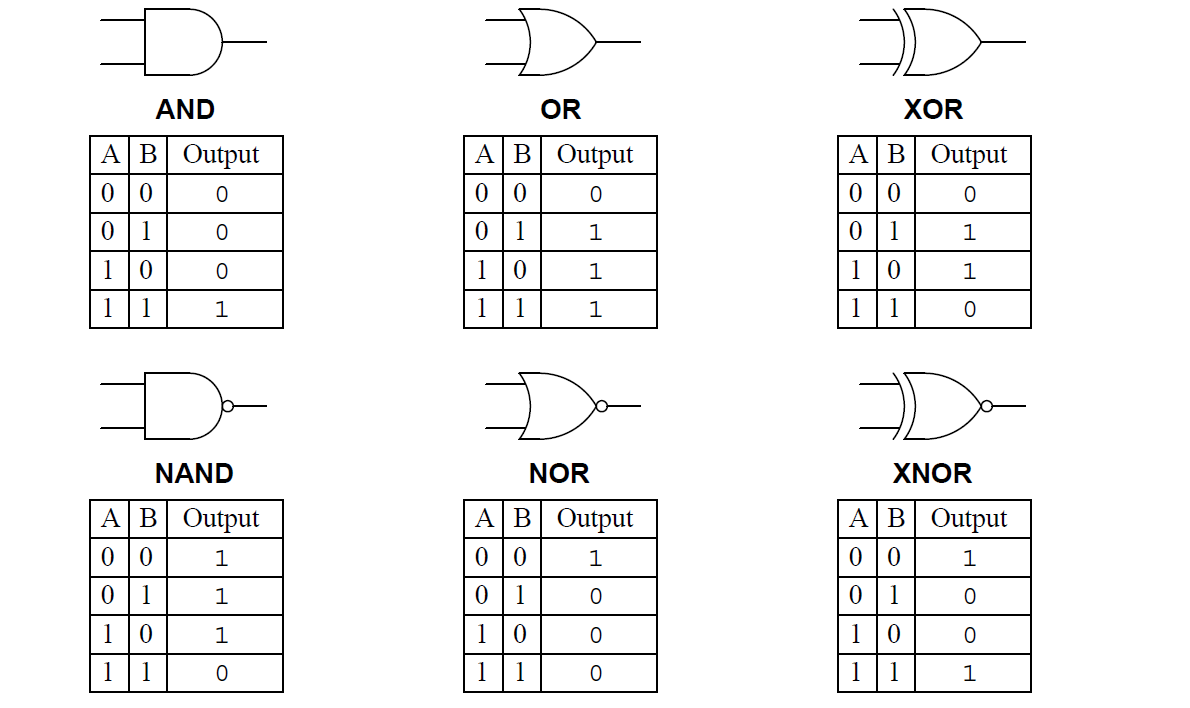
Hardware Description Language(HDL)
我们使用HDL语言描述相关门电路,以异或门为例,根据其真值表,我们可以得到异或门的布尔函数如下:
根据布尔函数,我们可以搭建对应的电路(假设我们已经根据与非门建立了与、非以及或电路):
下面我们来写一下异或门的HDL描述,分为如下几步:
- 搭建好门的框架,包括输入输出和门组成部分
1 | /* Xor gate: out = (a And Not(b)) Or (Not(a) And b)*/ |
- 用已经构建好的其他门,描述门的组成部分
1 | /* Xor gate: out = (a == b) ? 0 : 1 |
描述一般是从左到右的顺序。
多位逻辑总线
有些时候我们需要处理多位输入,此时需要将一组信号集成,构成总线,例如我们考虑一个16位的加法器
这里有两个16位输入,一个16位输出,该模块的HDL框架如下:
1 | /* Add16: add two 16-bit numbers */ |
再例如,我们可以设计一个Add4模块,将两个输入的4bit数进行And操作:
1 | /* And4: Computes a bit-wise and of its two 4-bit input buses */ |
在编写多位逻辑电路时,我们需要注意位数匹配,例如Add16,输出是16位,我们不能只输出15个
项目1:根据NAND搭建基本逻辑电路
项目简述
现在请根据NAND搭建如下电路:
| Not | And | Or | Xor |
|---|---|---|---|
| Mux | Dmux | Not16 | And16 |
| Or16 | Mux16 | Or8Way | Mux4Way16 |
| Mux8Way16 | DMux4Way | DMux8Way | Nand(基本) |
根据功能,我们可以将上面的chip分为如下几类:
| 基本逻辑门 | 16-bit 门变种 | 多路变种 |
|---|---|---|
| Not(已完成) | Not16(已完成) | Or8Way(已完成,将输入的8bit进行或操作) |
| And(已完成) | And16(已完成) | Mux4Way16(已完成,4选1) |
| Or(已完成) | Or16(已完成) | Mux8Way16(已完成,8选1) |
| Xor(已完成) | Mux16(已完成) | DMux4Way(已完成,1分4) |
| Mux(已完成) | DMux8Way(已完成,1分8) | |
| DMux(已完成) | - |
Mux和DMux
此处我们特别讲解一下Mux和DMux门
- 数据选择器(Multiplexer, Mux)
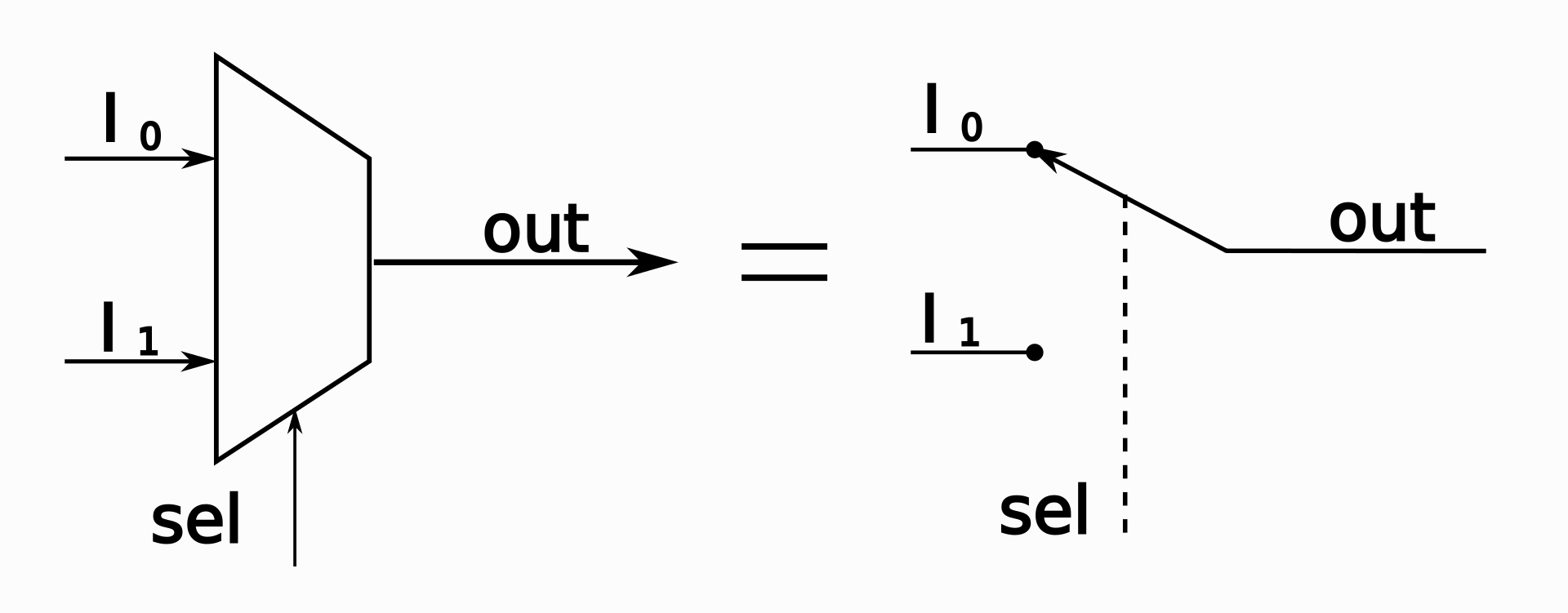
1 | // 可以看出,mux电路主要用于实现if逻辑 |
真值表如下:
| a | b | sel | out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
有了数据选择器之后,我们可以创建一些可编程门,例如AndMuxOr门
1 | if (sel == 0) |
- 数据分解器
和数据选择器正相反,数据分解器将一个数据进行拆分:
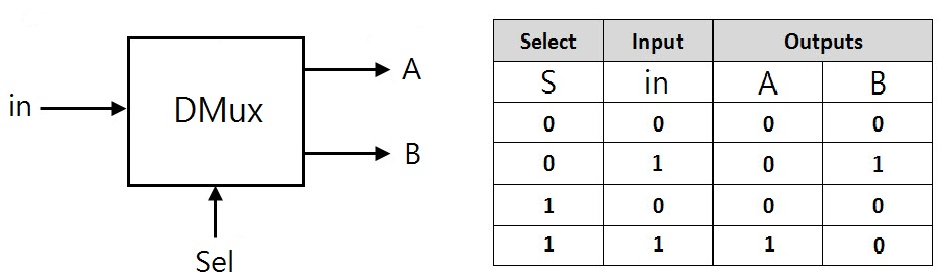
1 | if (sel == 0) |
- 多路数据选择器(Mux4Way16)
一个四路的16位数据选择器如下所示
1 | /** |
实际上我们只需要按照层层筛选的过程,先根据一位在ab和cd中各选出一个,再根据sel另一位做剩下的选择:
Example:实际上Mux和Dmux是构成网络交换机的重要组成部分,通过一根总线,即可传输多组数据,再根据不同的sel进行筛选分发
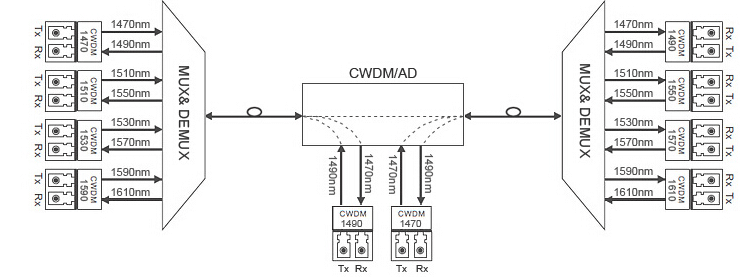
一个多路的Mux和DMux代码实现如下:
1 | /**************** Mux8Way16 (8 in 1 out) ****************/ |
这一章的实验并不难,下一节中,我们会用上面搭建好的逻辑门,构造一个基本加法器。