PID control and tuning

Abstract

This article summarizes the PID control method and tuning strategy of PID controller.

PID controller

What is PID controller

proportional–integral–derivative (PID) controller is a control loop which employs feedback, the block diagram of a PID controller is shown below:

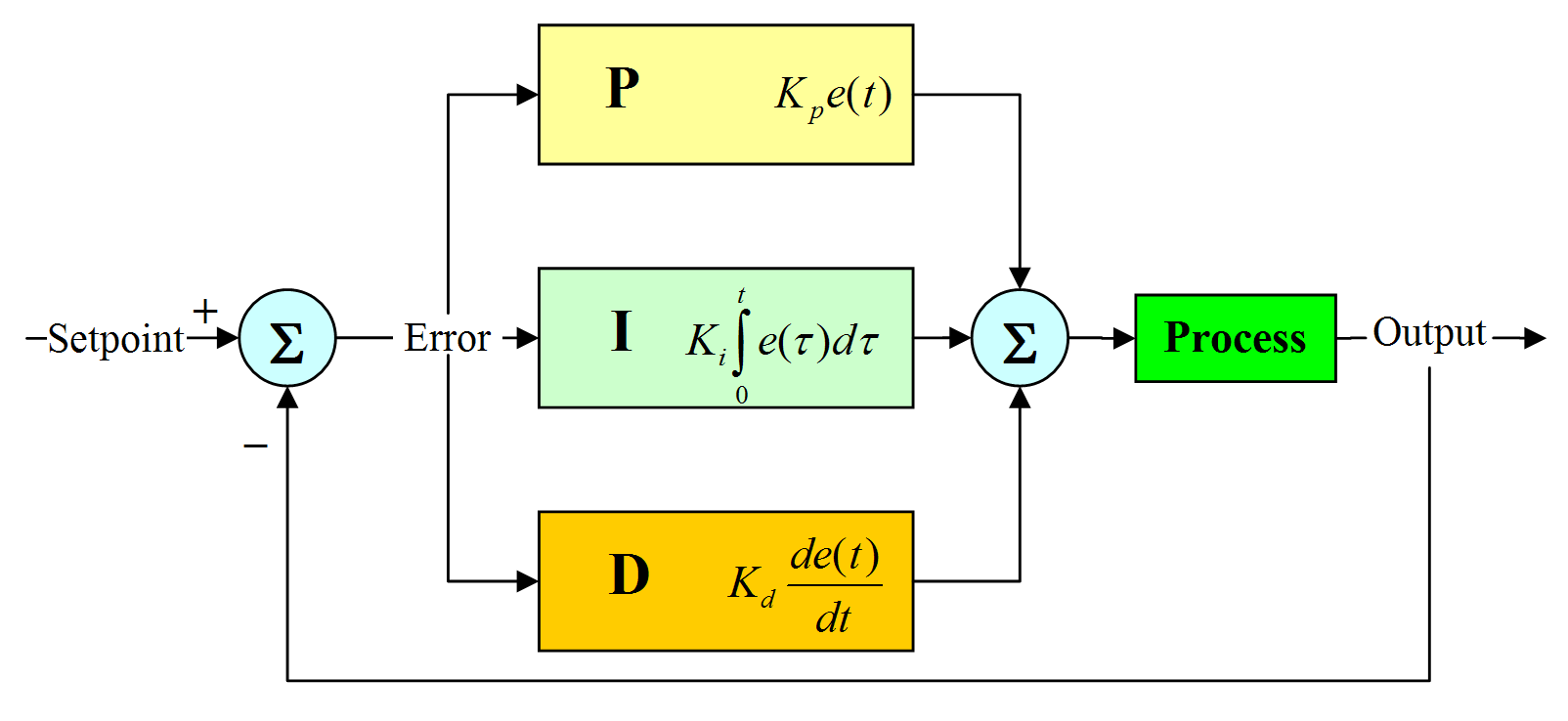
• Term P is proportional to system error $e(t)$，if the error is large and positive, then the control output will be proportionately large and positive, use P alone shall causes the steady state error since it needs an error to generate response.
• Term I looks for the past error or the system, after the application of proportional control, there will be a residual error, and our integral controller will work to eliminate the residual error due to the historic cumulative value of the error.
• Term D estimates the future trend of the error based on current changing rate. The more rapid the change, the greater the controlling or dampening effect.

Mathematical form of PID

• Continuous form

$$u(t)=K_p(e(t)+\frac{1}{T_i}\int_{0}^{t}e(\tau)d\tau+T_d\frac{de(t)}{dt})$$

• Discrete form

$$u(k)=K_p(e(k)+\frac{T}{T_i}\sum e(j)+\frac{T_d}{T}(e(k)-e(k-1) ) )$$

Why we use PID controller

1. Simple
2. Good performace

how to turn a PID controller (Important)

To implement the PID controller, it normally means to determine the three parameters, this is also called the PID tuning. This section will discuss how to tuning the PID controller

Method 1 manual tuning

To implement manual tuning, first we need to know the effect of increasing the PID gains on step response.

PID gain	Percent Overshoot	Settling time	Steady-state error
Increasing $K_P$	Increases	-	Decreases
Increasing $K_I$	Increases	Increases	Zero steady-state error
Increasing $K_D$	Decreases	Decreases	-

A commonly used manual tuning method:

Assume we want to adjust a system shown below where $b=10,\zeta = 0.707$ and $\omega_n=4$.

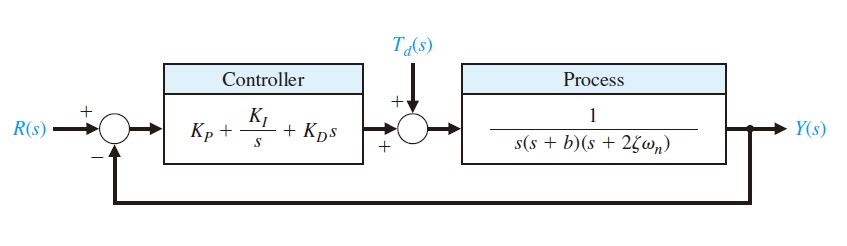
1. Set $K_I$ and $K_D$ to 0
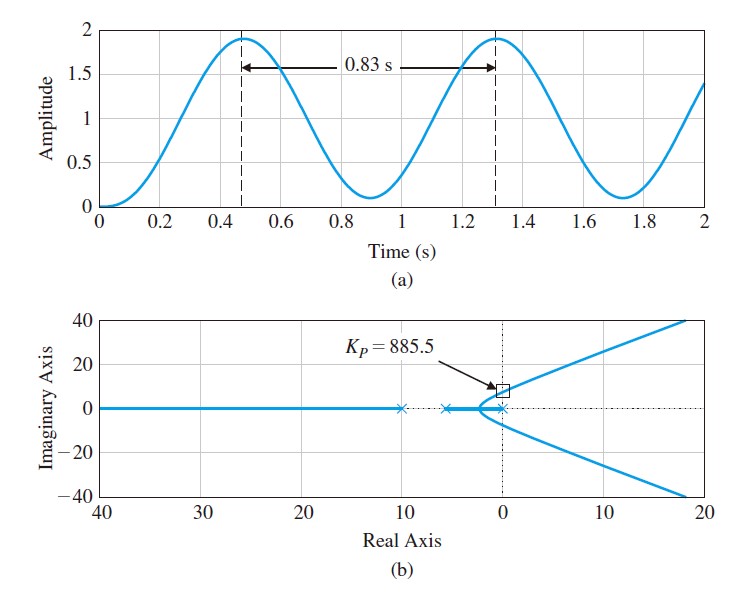
2. Increasing $K_P$ slowly until the output of the closed-loop system oscillates just on the edge of instability. Here $K_p=885.5$.

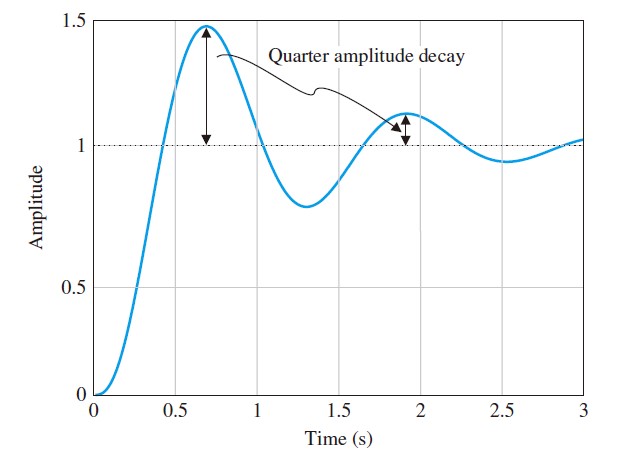
1. Reduce $K_p$ to achieve quarter amplitude decay, Here $K_p=370$.

1. Increasing $K_D$ to decrease setting time and overshoot.
2. Increasing $K_I$ to eliminate steady-state error.

Method 2 auto tuning

In SImulink, it provides a auto tuning method of three parameters in PID controller by selecting proper performance index, then it will generate proper PID parameters automatically.

• Response Time (Bandwidth): Increasing the response time increases the oscillation intensity of the system output.
• Transient Behavior (Phase Margin): Increasing the transient behavior increases the robustness of the system.

Reference

---

1. 1.Wikipedia about PID ↩
2. 2.Modern Control Systems by Richard C. Dorf ↩