模型参考自适应控制

摘要

在实际物理世界中，任何一个系统都是非线性的，都不是理想的物理模型。因此针对非理想的模型，我们希望能够设计出一种控制器，使其能够有效处理系统非线性及不确定量，从而在一定程度上使其响应接近于理想模型。模型参考自适应控制（Model reference adaptive control, MRAC）就是基于这个目标提出的，本文将针对模型参考自适应控制（MRAC）过程进行总结。

基本控制策略

目前常见的控制策略主要有两种

Robust Control：参数是固定的，系统对参数变化不敏感，如果在最坏的情况下，系统仍然能够具有良好的响应，那么系统就是robust的。
Adaptive Control：参数可以在线调整，系统能够随着外部扰动，及时改变参数，从而达到良好的控制效果。

模型参考自适应控制原理

控制器组成

模型参考自适应控制器由两部分组成

参考模型（理想被控对象，可以通过指定控制性能确定）
控制器（参数可变）
参数调整机构（使用一种时变非线性算法，调整控制器参数）

控制目标

将参考模型的输出与被控对象输出的误差调整至最小，这样可以认为我们的被控对象与参考模型表现形式一致。

控制器设计过程

被控对象数学模型建立

被控对象的动力学方程

$\dot{x}_p=A_px_p+B_p\lambda u+B_p\delta_p(x_p),\ x_p(0)=x_{p0}$

$A_p$和$B_p$是已知参数，$x_p$可测的（状态反馈），$u$是控制变量，$\lambda$是未知参数，可以表示为：

$\lambda =\begin{bmatrix} \lambda_1>0 & & \\ & ... & \\ & & \lambda_m>0 \end{bmatrix} \in \mathbb{R}^{m\times m}$

如果$\lambda$对角线元素有0，那么就是不可控情况，因为这个分量会使对应的控制量清零。

$\delta_p(x_p)$是非线性系统不确定量，几个关键变量所属线性空间为：

$x_p \in \mathbb{R}^{n_p}\\ u \in \mathbb{R}^{m}\\ \delta _p:\mathbb{R}^{n_p}\rightarrow \mathbb{R}^{m}$

考虑$B_p\lambda u+B_p\delta_p(x_p)$，我们可以将其写为

$B_p\lambda [u+\lambda^{-1}\delta_p(x_p)]$

从上式可以看出，$u$可以影响$\delta_p(x_p)$的每一部分，这个叫做匹配系统。如果不能，那就是非匹配系统。

$\delta_p(x_p)$可以进一步写为

$\delta _p(x_p)=W^{T}_p\sigma _p(x_p)$

其中$W^{T}_p$是未知部分，$\sigma _p(x_p)$是已知部分

$W_p \in \mathbb{R}^{s\times m} \\ \sigma _p:\mathbb{R}^{n_p}\rightarrow \mathbb{R}^{s}$

$\sigma _p(x_p)$可以进一步写为：

$\sigma_p (x_p)=[\sigma_{p1}(x_1),...,\sigma_{ps}(x_p)]$

我们假设$\sigma{p1}$到$\sigma{ps}$是Locally Lipschitz函数。

实例

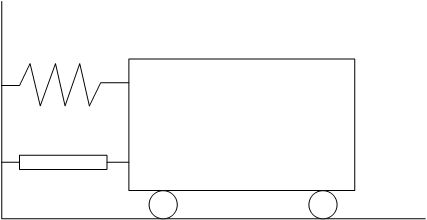
考虑一个带有阻尼和弹簧的小车，对小车施加一个向前的控制力$u$，则

$m\ddot{p}=u-\alpha p - \beta \dot{p}$

假设我们并不知道$\alpha$和$\beta$的值，令

$x_p=\begin{bmatrix} x_{p1}\\ x_{p2} \end{bmatrix}$

其中

$x_{p1}=p\\ x_{p2}=\dot{p}$

则

$\begin{aligned} \dot{x}_{p1}&=x_{p2}\\ \dot{x}_{p2}&=\frac{u}{m}-\frac{\alpha}{m}x_{p1}-\frac{\beta}{m}x_{p2} \end{aligned}$

可得到下式

$\dot{x}_p=\begin{bmatrix} 0 &1 \\ 0 &0 \end{bmatrix}x_p+\begin{bmatrix} 0\\ 1 \end{bmatrix}(1/m)u+\begin{bmatrix} 0\\1 \end{bmatrix}\begin{bmatrix} -\alpha/m\\-\beta/m \end{bmatrix}^T\begin{bmatrix} x_{p1}\\ x_{p2} \end{bmatrix}$

其中

$\begin{aligned} A_p &=\begin{bmatrix} 0 &1 \\ 0 &0 \end{bmatrix}\\ B_p &=\begin{bmatrix} 0\\ 1 \end{bmatrix}\\ \lambda &= 1/m\\ W^{T}_{p}&=\begin{bmatrix} -\alpha/m\\-\beta/m \end{bmatrix}^T\\ \sigma_p&=\begin{bmatrix} x_{p1}\\ x_{p2} \end{bmatrix} \end{aligned}$

在某些情况下，我们甚至不知道$\sigma_p$，我们可以使用拟合方式进行建模。

控制模型建立

现在我们已知被控对象和控制量分别为：

$\begin{aligned} \dot{x}_p&=A_px_p+B_p\lambda u+B_pW^{T}_p\sigma_p(x_p),\ x_p(0)=x_{p0}\\ u&=u_n+u_a \end{aligned}$

$u_n$和$u_a$分别为常规控制量和自适应控制量，我们先考虑最简单的情况：$\lambda$是一个单位矩阵，而$B_pW^{T}_p\sigma_p(x_p)$为0（考虑状态空间表达式$\dot{x}=Ax+Bu$，我们不希望后面跟了一堆累赘），此时

$\begin{aligned} \dot{x}_p&=A_px_p+B_p u\\ u&=u_n=-K_1x_p+K_2c \end{aligned}$

控制量由状态反馈和前馈部分组成

$\begin{aligned} K_1&\in \mathbb{R}^{m\times n_p}\\ K_2&\in \mathbb{R}^{m\times n_c}\\ c&\in \mathbb{R}^{n_c} \end{aligned}$