Parzen窗函数法

Parzen窗函数法是一种广泛应用的非参数估计方法（所谓非参数，就是这样的方法不需要对样本分布做出任何预先假设³），用于估计给定样本点的概率密度函数。

一张图解释窗函数法

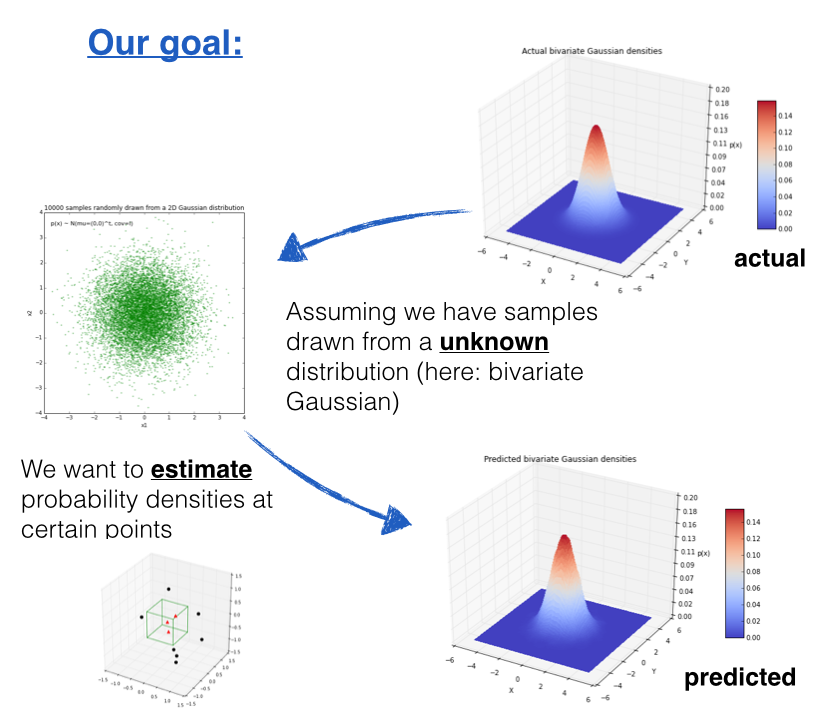
上面这个图就描述了窗函数法的目标：

窗函数法的基础是数数，我们要数有多少个样本落在了指定的区域$R_n$中，这个区域叫做Window，根据我们的经验，落入样本的概率为：

$P(x)=\frac{\#\ of\ samples\ in\ R}{total\ samples}$

现在，考虑我们的一个样本点$\boldsymbol{x}$，以及一个包围它的非常小的领域$R$，它的体积为$V$，则：

$p(x)V=\int_{R}p\left ( u \right )\mathrm{d}u$

这是连续平滑函数的形式，如果是离散形式，那么我们可以得到如下公式：

$\hat{p}\left ( \boldsymbol{x} \right )\approx \frac{k/n}{V}$

这个体积太小太大都不行，太小会导致不稳定，太大则过于平滑，对于这个矛盾，我们采用下面两种方法来调节：

从上面我们可以看出，Parzen和k近邻，都不需要预先对样本分布有任何假设，所以是模型无关。但是模型无关是有代价的，虽然不需要预先假设，但也意味着一般情况下我们的数据不能太过复杂，高维情况会出现维数灾难。

上节提到，我们需要选择一个合适的包围$\boldsymbol x$的足够小区域，我们可以选择立方体作为这个区域，考虑一个$d$维度的超立方体，它的边长$h(n)$是样本数$n$的函数，则该区域体积为：

$V(n)=h^d(n)$

定义如下计数函数：

$\varphi(\boldsymbol x)=\left\{\begin{matrix} 1\ \ \ \ \ \ \ 在区域内\\ 0\ \ \ \ 不在区域内 \end{matrix}\right.$

那么落在区域内的样本点个数可以表示为（这里我们进行了一个比例尺变换，即除以$h(n)$）：

$k(n)=\sum_{i=1}^{n}\varphi(\frac{x-x_i}{h(n)})$

代入到上面的计算概率密度的公式中：

$\hat{p}\left ( \boldsymbol{x},n \right )=\frac{1}{nV}\sum_{i=1}^{n}\varphi(\frac{x-x_i}{h(n)})$

从上式中可知，如果领域内集中大量样本点，那么得到的概率密度会很大，否则会很小。