Convex optimization

This article will discuss about the convex optimization problem.

Basic of constrained optimization¹

So here’s our optimization problem with constrains:

$$\begin{equation} \begin{array}{cl}{\min _{x}} & {f(x)} \\ {\text { s.t. }} & {g(x) \leq 0}\end{array}\\ x \in \mathbb{R}^{n}, f: \mathbb{R}^{n} \rightarrow \mathbb{R}, g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} \end{equation} \label{constrains}$$

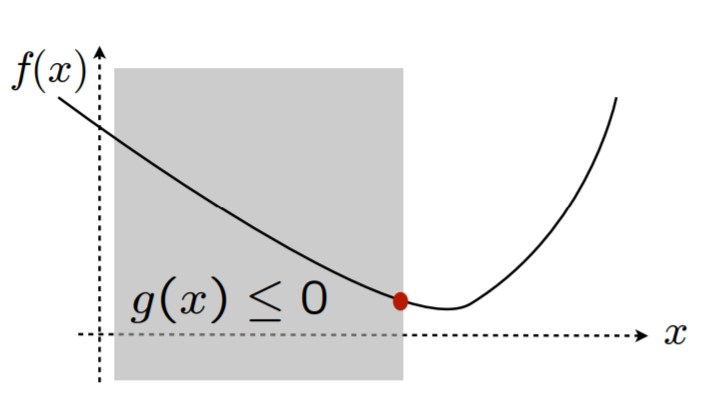
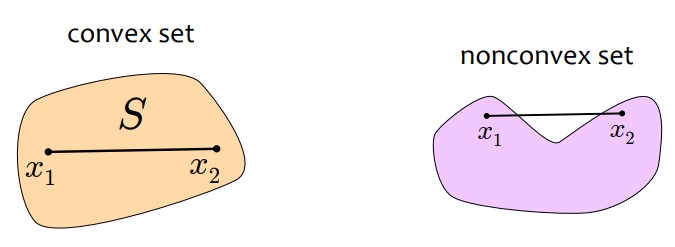
Convex sets and functions

A set $S\subseteq \mathbb{R}^n$ is convex if for all $x_1,x_2\in S$

$$\lambda x_{1}+(1-\lambda) x_{2} \in S, \forall \lambda \in[0,1]$$

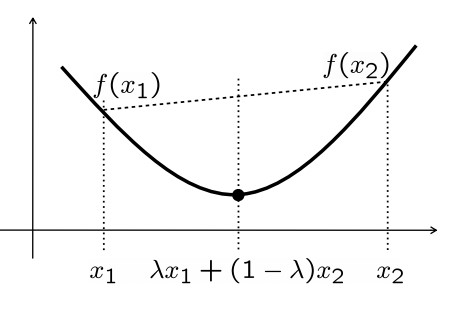
A convex function means $f:S\to \mathbb R$ is a convex function if $S$ is convex and

$$\begin{equation} \begin{aligned} f\left(\lambda x_{1}+(1-\lambda) x_{2}\right) \leq & \lambda f\left(x_{1}\right)+(1-\lambda) f\left(x_{2}\right) \\ & \forall x_{1}, x_{2} \in S, \lambda \in[0,1] \end{aligned} \end{equation}$$

The convex optimization problem

$$\begin{equation} \begin{array}{cl}{\min } & {f(x)} \\ {\text { s.t. }} & {x \in S}\end{array} \end{equation}$$

is a convex optimization problem if $S$ is a convex set and $f$ is a convex function.

In a convex optimization problem, every local solution is also a global one

Further reading

Please refer to linear mpc slides for a further reading

Reference

---

1. 1.A course from Alberto Bemporad ↩