哈希

Posted on | In ,

本文将针对哈希（散列）相关知识进行讲解。

介绍

所谓哈希（这个翻译真是太扯了），就是一个字典型数据结构，用于维护具有键值的数据结构，基本操作包括

  • 插入：如果key已经存在，进行覆盖
  • 删除
  • 搜索：给定key，返回对象，或者报告对象不存在（Hash miss）

这些操作可以通过AVL树实现，复杂度为$O(\lg n)$

Hash实现

最简单的实现

考虑最简单的情况，使用直接访问表，将对象保存在一段连续空间中，键值就是数组索引，这个实现有两个缺点

  • 键值如果不是整数，就不能作为索引
  • 空间效率很低，需要巨量的空间

具体实现

本节请参考，在Python中，hash的实现为dict

  • D[key] ~ search
  • D[key] = val ~ insert
  • del D[key] ~ delete

Hash常见应用场景

O(1)时间检索

由于哈希搜索的高效性，一般看到需要常数时间内的索引时，都会考虑使用哈希表。例如：

  • 文本索引/子字符串/文本推荐
  • 数据库
  • 网络路由/服务器
  • 文件/目录同步
  • 密码学

变位映射

变位映射（LeetCode760）给定两个列表 Aand B，并且 B 是 A 的变位（即 B 是由 A 中的元素随机排列后组成的新列表）。我们希望找出一个从 A 到 B 的索引映射 P 。一个映射 P[i] = j 指的是列表 A 中的第 i 个元素出现于列表 B 中的第 j 个元素上。即寻找A中某个元素在B中位置

双向映射

在有些问题中，我们需要找到一一对应的双向映射，即不仅能从A搜索到B，还要能从B搜索到A，此时我们采用两个哈希表分别记录字典，然后依次检索，模板如下：

1
2
3
4
if (amap.find(n[i]) != amap.end() && amap[n[i]] != v[i])  //从n到v的映射
    return false;
if (bmap.find(v[i]) != bmap.end() && bmap[v[i]] != n[i])  //从v到n的映射
    return false;

哈希表的问题及解决方案

哈希冲突

产生原因

哈希函数产生的哈希值是有限的，而当数据较多，可能导致不同数据对应相同哈希值，产生哈希冲突。

解决方案

开放地址方法

产生哈希冲突时，进行偏移或干脆采用随机方法，直至冲突消失。

链式地址法

相同哈希值使用链表进行连接

建立公共溢出区

建立一块公共区域，专门存放所有哈希冲突的数据

再哈希法

对冲突的哈希值再进行哈希，直到无冲突为止

哈希miss

附录

散列索引（原理性讲解，可不看）

静态散列

数据桶的个数固定，通过添加溢出页，处理溢出问题。这种方式比较简单，但是在已满桶中插入数据项，就需要增加一个溢出页，如果不希望增加溢出，一个解决方案为修改散列函数，将桶数目扩大，如下图所示：

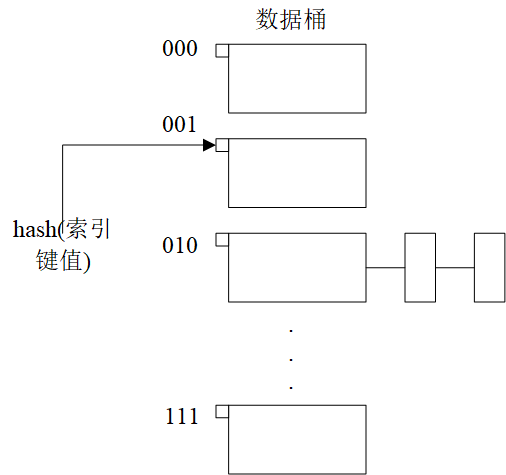
一个散列索引表如上图所示：其中，桶采用二进制进行编码，如果加一位，会翻一倍（类似vector增长），这个增长过程带来的问题：可能会导致数据的大规模调整。

可扩展的动态散列

直接扩展桶可能导致大规模重组，一个解决方案是引入一个仅仅存储桶指针的目录数组，通过翻倍目录项的方式取代翻倍数据桶数目，每次只分裂有溢出的桶。翻倍目录项比翻倍数据桶要简单很多。

.png)

在这种扩展策略中，有目录项指向数据桶，目录项有编号，当有一个桶满了后（例如B桶），就将目录项复制，然后复制的目录项依次指向对应的桶。满了的桶要分裂，令目录项指向他。同时，分裂的桶要加一个资格位，对两个桶进行区分。这样分裂下去的一个结果是，可能有多个指针指向同一个桶。

可扩展散列基本技术
  • 引入散列函数$h$，将索引键值映射为2进制，并解释最后$d$位；其中$d$是目录项编码位数，也叫全局位深度，目录项总数为$2^d$个。
  • 每个桶包含局部位深度$l$，即所存储数据项后$l$位相同，例如5和21，当深度为2时，其二进制后两位分别为01，一般情况下，有$2^{d-l}$个目录项指向该桶，当$l=d$时，只有一个目录项指向这个桶，起初$l=d$。
  • 当向一个满的、局部位深度为$l$的桶插入数据项时要分裂，其局部位深度变为$l+1$，若$l+1>d$，目录翻倍。
  • 目录项翻倍即将原有目录复制产生一个新目录，然后调整目录编号，新目录与旧目录在新扩展的比特位上取值不同，新旧目录指向同一个桶，只是在桶分裂后，新旧目录分别指向原桶和分裂桶。

线性散列

线性散列可扩展，且不需要目录项，允许灵活地选择分裂时机，但缺点是如果数据项键值散列后分布不均匀的倾斜度大，导致的问题可能比扩展散列还严重。

0%