多叉树

Posted on | In ,

Listen, a tree is growing

有两个以上节点的树叫做多叉树。

B树家族

B树的典型应用是磁盘信息的存储，如果采用二叉树，会导致存储的信息过于分散，从而增大读取时间。

B树

B树操作

  • 查找操作

  • 插入操作

在插入过程中，会遇到三种情况：

  1. 键值放入有空间的叶节点中

这种情况直接把值放进去就可以。

  1. 要插入键值的叶节点已经满了

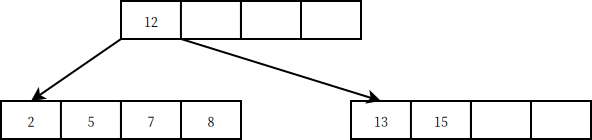
向一个满叶节点中插入数字6

第一步，分裂叶节点，创建一个新叶节点，然后将已经慢了的一半键值转移至新叶节点中

节点分裂

第二步，将中间值放入父节点中，然后在父节点中放置一个指向新节点的指针，这里的中间值为6

将中间值6放入父节点中，如果父节点已经满了，那么继续分裂

  1. 一种特殊情况，B树的根节点满了，这是唯一一个会引起B树高度增长的情况

  • 删除操作
  1. 如果删除键值K后，叶节点保持半满，那么直接删除即可
  2. 如果不能保持半满，会引起下溢

B*树

B*树是B树的一种变种，要求除了根节点至少$2/3$满

B+树

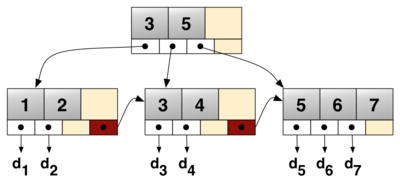
什么是B+树

B+树可以简单理解为：叶节点是数据，内部节点是索引集。

  • 内部节点：存储键值、键值数量及指针
  • 叶节点：存储键值、数据文件中与键值对应的引用以及指向下一叶节点的指针

B+树的技术特点与约束

  • 阶数$m$，每个节点中最多键值数，即上图一个大节点中的键值个数
  • 半满约束，内节点键值最少为$\left \lfloor \frac{m}{2}+1 \right \rfloor$，即半满状态，当然根节点除外，根节点可以只有一个键值
  • 每个节点对应一页的大小

B+树操作

  1. 搜索算法
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    func tree-search(nodePointer, search-key-value K) return nodePointer
        if *nodePointer 是叶节点 then
            return nodePointer;
        else
            if K<K1 then
                return tree_search(P[0],K);
            else if K >= Kn then
                return tree_search(P[n],K);
            else 
                find i such that Ki<=K<=Ki+1
                return tree_search(Pi,K);
            endif
        endif
    endfunc;

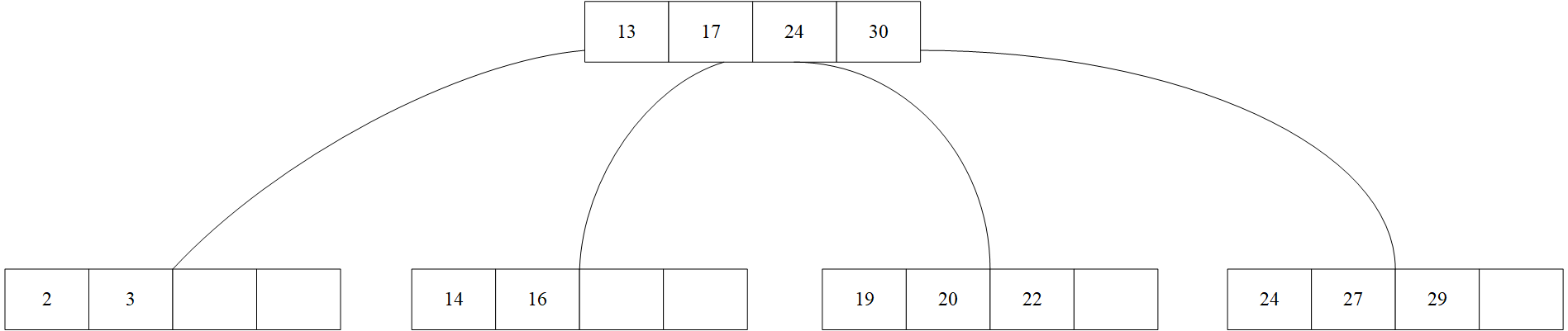
从上面的图可知，节点中的值是进行排序的，且小于父节点中的值。

  1. 插入算法（节点分裂）

以上图为例，插入18，可以发现节点未满，直接将18放入节点即可

插入8，发现需要被插入的节点已经满了，因此需要创建一个新的节点，来放置新的值，同时由于第一个节点已经满了，因此将节点1中的一半的值放进新节点中。

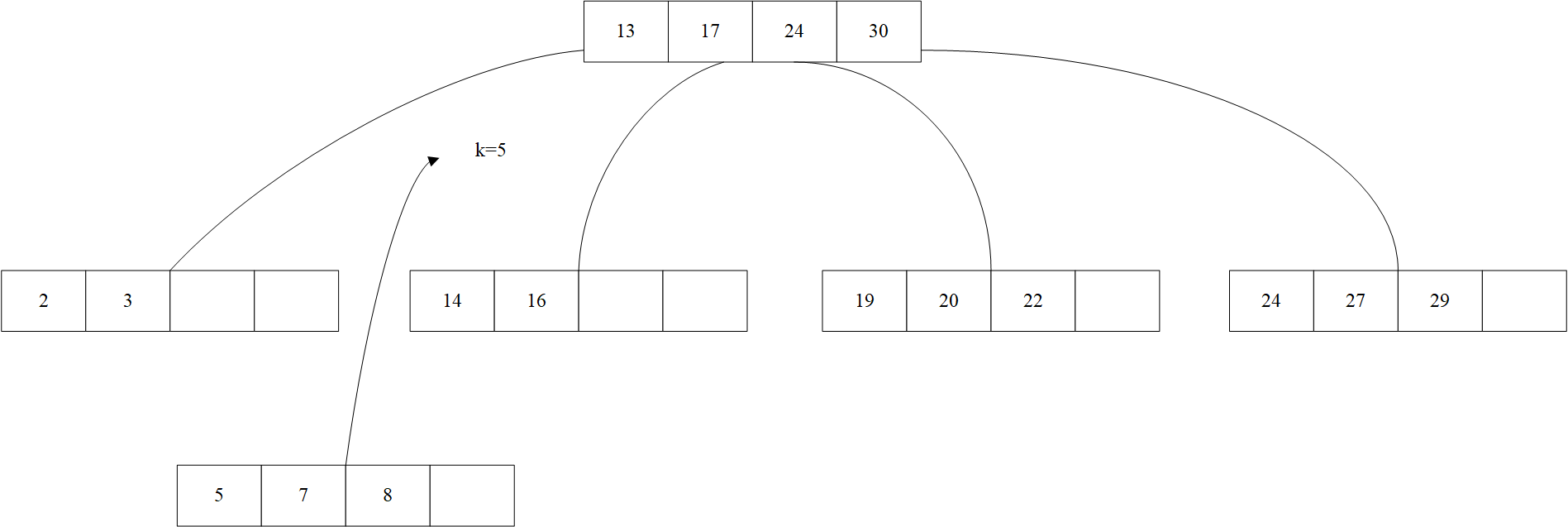
然后多了一个节点需要处理，有一个指针引向了上层，然而发现根节点已经没有位置了，就需要对根节点进行分裂，提出中间值作为根节点，然后将剩下的值进行分裂。

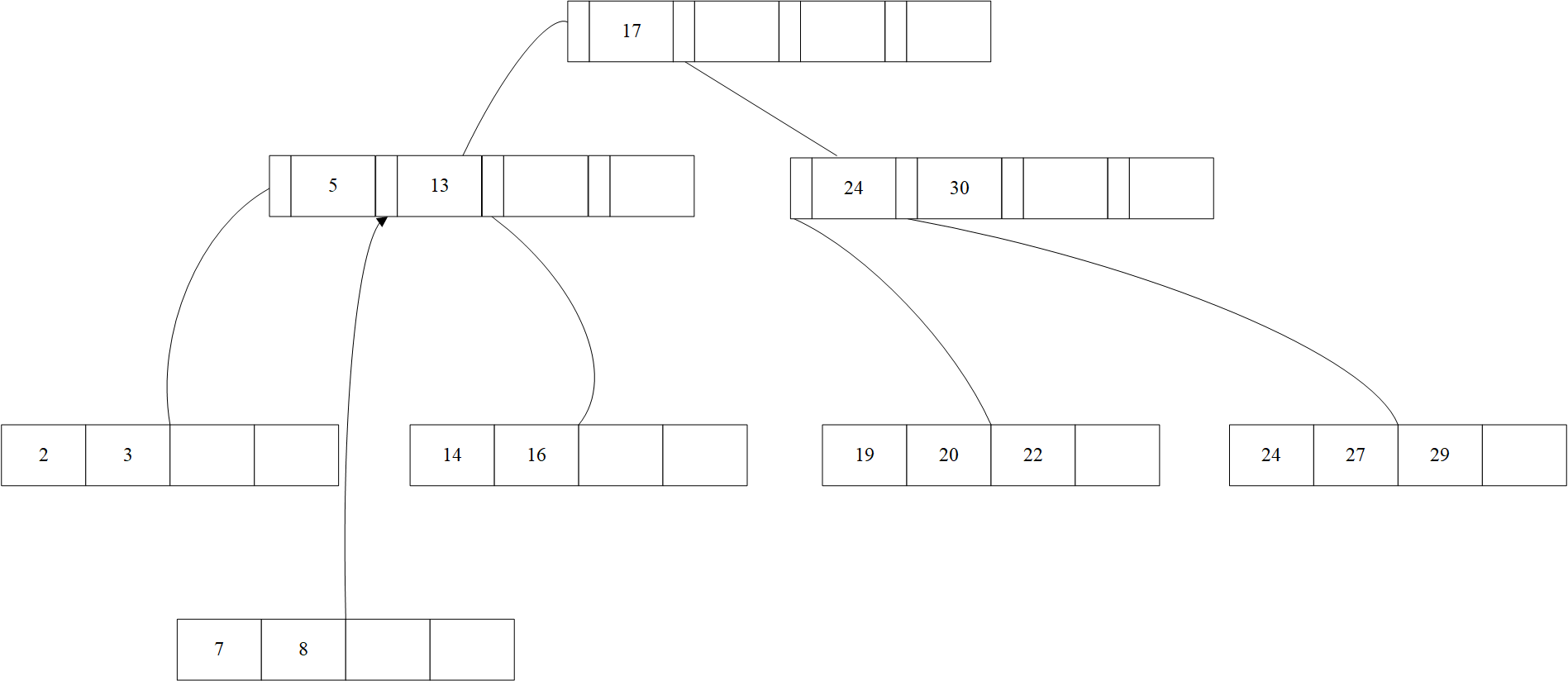
可以看到树深度增加了。B+树的插入算法如下所示：

点击显/隐
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
// C++ program for B-Tree insertion 
#include<iostream> 
using namespace std; 

// A BTree node 
class BTreeNode 
{ 
    int *keys; // An array of keys 
    int t;	 // Minimum degree (defines the range for number of keys) 
    BTreeNode **C; // An array of child pointers 
    int n;	 // Current number of keys 
    bool leaf; // Is true when node is leaf. Otherwise false 
public: 
    BTreeNode(int _t, bool _leaf); // Constructor 

    // A utility function to insert a new key in the subtree rooted with 
    // this node. The assumption is, the node must be non-full when this 
    // function is called 
    void insertNonFull(int k); 

    // A utility function to split the child y of this node. i is index of y in 
    // child array C[]. The Child y must be full when this function is called 
    void splitChild(int i, BTreeNode *y); 

    // A function to traverse all nodes in a subtree rooted with this node 
    void traverse(); 

    // A function to search a key in the subtree rooted with this node. 
    BTreeNode *search(int k); // returns NULL if k is not present. 

// Make BTree friend of this so that we can access private members of this 
// class in BTree functions 
friend class BTree; 
}; 

// A BTree 
class BTree 
{ 
    BTreeNode *root; // Pointer to root node 
    int t; // Minimum degree 
public: 
    // Constructor (Initializes tree as empty) 
    BTree(int _t) 
    { root = NULL; t = _t; } 

    // function to traverse the tree 
    void traverse() 
	{ if (root != NULL) root->traverse(); } 

    // function to search a key in this tree 
    BTreeNode* search(int k) 
	{ return (root == NULL)? NULL : root->search(k); } 

    // The main function that inserts a new key in this B-Tree 
    void insert(int k); 
}; 

// Constructor for BTreeNode class 
BTreeNode::BTreeNode(int t1, bool leaf1) 
{ 
    // Copy the given minimum degree and leaf property 
    t = t1; 
    leaf = leaf1; 

    // Allocate memory for maximum number of possible keys 
    // and child pointers 
    keys = new int[2*t-1]; 
    C = new BTreeNode *[2*t]; 

    // Initialize the number of keys as 0 
    n = 0; 
} 

// Function to traverse all nodes in a subtree rooted with this node 
void BTreeNode::traverse() 
{ 
    // There are n keys and n+1 children, travers through n keys 
    // and first n children 
    int i; 
    for (i = 0; i < n; i++) 
    { 
        // If this is not leaf, then before printing key[i], 
        // traverse the subtree rooted with child C[i]. 
        if (leaf == false) 
            C[i]->traverse(); 
        cout << " " << keys[i]; 
    } 

    // Print the subtree rooted with last child 
    if (leaf == false) 
        C[i]->traverse(); 
} 

// Function to search key k in subtree rooted with this node 
BTreeNode *BTreeNode::search(int k) 
{ 
    // Find the first key greater than or equal to k 
    int i = 0; 
    while (i < n && k > keys[i]) 
        i++; 

    // If the found key is equal to k, return this node 
    if (keys[i] == k) 
        return this; 

    // If key is not found here and this is a leaf node 
    if (leaf == true) 
        return NULL; 

    // Go to the appropriate child 
    return C[i]->search(k); 
} 

// The main function that inserts a new key in this B-Tree 
void BTree::insert(int k) 
{ 
    // If tree is empty 
    if (root == NULL) 
    { 
        // Allocate memory for root 
        root = new BTreeNode(t, true); 
        root->keys[0] = k; // Insert key 
        root->n = 1; // Update number of keys in root 
    } 
    else // If tree is not empty 
    { 
        // If root is full, then tree grows in height 
        if (root->n == 2*t-1) 
        { 
            // Allocate memory for new root 
            BTreeNode *s = new BTreeNode(t, false); 

            // Make old root as child of new root 
            s->C[0] = root; 

            // Split the old root and move 1 key to the new root 
            s->splitChild(0, root); 

            // New root has two children now. Decide which of the 
            // two children is going to have new key 
            int i = 0; 
            if (s->keys[0] < k) 
                i++; 
            s->C[i]->insertNonFull(k); 

            // Change root 
            root = s; 
        } 
        else // If root is not full, call insertNonFull for root 
            root->insertNonFull(k); 
    } 
} 

// A utility function to insert a new key in this node 
// The assumption is, the node must be non-full when this 
// function is called 
void BTreeNode::insertNonFull(int k) 
{ 
    // Initialize index as index of rightmost element 
    int i = n-1; 

    // If this is a leaf node 
    if (leaf == true) 
    { 
        // The following loop does two things 
        // a) Finds the location of new key to be inserted 
        // b) Moves all greater keys to one place ahead 
        while (i >= 0 && keys[i] > k) 
        { 
            keys[i+1] = keys[i]; 
            i--; 
        } 

        // Insert the new key at found location 
        keys[i+1] = k; 
        n = n+1; 
    } 
    else // If this node is not leaf 
    { 
        // Find the child which is going to have the new key 
        while (i >= 0 && keys[i] > k) 
            i--; 

        // See if the found child is full 
        if (C[i+1]->n == 2*t-1) 
        { 
            // If the child is full, then split it 
            splitChild(i+1, C[i+1]); 

            // After split, the middle key of C[i] goes up and 
            // C[i] is splitted into two. See which of the two 
            // is going to have the new key 
            if (keys[i+1] < k) 
                i++; 
        } 
        C[i+1]->insertNonFull(k); 
    } 
} 

// A utility function to split the child y of this node 
// Note that y must be full when this function is called 
void BTreeNode::splitChild(int i, BTreeNode *y) 
{ 
    // Create a new node which is going to store (t-1) keys 
    // of y 
    BTreeNode *z = new BTreeNode(y->t, y->leaf); 
    z->n = t - 1; 

    // Copy the last (t-1) keys of y to z 
    for (int j = 0; j < t-1; j++) 
        z->keys[j] = y->keys[j+t]; 

    // Copy the last t children of y to z 
    if (y->leaf == false) 
    { 
        for (int j = 0; j < t; j++) 
            z->C[j] = y->C[j+t]; 
    } 

    // Reduce the number of keys in y 
    y->n = t - 1; 

    // Since this node is going to have a new child, 
    // create space of new child 
    for (int j = n; j >= i+1; j--) 
        C[j+1] = C[j]; 

    // Link the new child to this node 
    C[i+1] = z; 

    // A key of y will move to this node. Find the location of 
    // new key and move all greater keys one space ahead 
    for (int j = n-1; j >= i; j--) 
        keys[j+1] = keys[j]; 

    // Copy the middle key of y to this node 
    keys[i] = y->keys[t-1]; 

    // Increment count of keys in this node 
    n = n + 1; 
} 

// Driver program to test above functions 
int main() 
{ 
    BTree t(3); // A B-Tree with minium degree 3 
    t.insert(10); 
    t.insert(20); 
    t.insert(5); 
    t.insert(6); 
    t.insert(12); 
    t.insert(30); 
    t.insert(7); 
    t.insert(17); 

    cout << "Traversal of the constucted tree is "; 
    t.traverse(); 

    int k = 6; 
    (t.search(k) != NULL)? cout << "\nPresent" : cout << "\nNot Present"; 

    k = 15; 
    (t.search(k) != NULL)? cout << "\nPresent" : cout << "\nNot Present"; 

    return 0; 
}

删除算法（节点合并）

B与B+树的区别

B+树是B树的延伸，他们的主要区别如下

B Tree B+ Tree
数据存放在叶节点和普通节点中 数据只存放在叶节点中
搜索速度较慢 搜索速度较快
不需要额外的索引键 需要保存额外的索引键
删除操作很复杂 删除操作比较简单，因为数据可以直接从叶节点中删除
叶节点相互之间没有连接 叶节点通过链表方式进行连接，从而便于遍历操作

字典树（前缀树）

字典树的定义

Trie树，即字典树，又称单词查找树或键树，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。字典树的基本原理就像查询字典一样，因此可以快速定位单词，非常高效。

字典树的性质

  1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
  2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
  3. 每个节点的所有子节点包含的字符都不相同。

字典树及其方法的实现

下面给出一种常用字典树及其方法的实现，包括添加单词和搜索单词两种操作，字典树类成员变量如下：

1
2
3
4
private:
    vector<Trie*> children;  //子节点，每个节点都是一个Trie* 结构
    bool is_end;             //用于判断一棵分支是否已经到达叶节点
    static const int R = 26;

一些基本成员函数如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Trie() : children{vector<Trie*>(R)},
         is_end{false} {
}

bool contain_key(char ch){                      //当前节点为根节点下是否包含字符ch
    return children[ch - 'a'] != nullptr;
}

Trie* get(char ch){                   //返回子树
    return children[ch - 'a'];
}

void put(char ch, Trie* node) {       //将node拼接至节点下
    children[ch -'a'] = node;
}

void set_end() {
    is_end = true;
}

bool get_is_end(){
    return is_end;
}

插入键

我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况：

  • 链接存在。沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
  • 链接不存在。创建一个新的节点，并将它与父节点的链接相连，该链接与当前的键字符相匹配。

重复以上步骤，直到到达键的最后一个字符，然后将当前节点标记为结束节点，算法完成。

1
2
3
4
5
6
7
8
9
10
11
void insert(string word) {
    Trie* node = this;
    for(char &ch : word){
        int idx = ch - 'a';
        if(node->children[idx] == nullptr){
            node->children[idx] = new Trie();
        }
        node = node->children[idx];
    }
    node->is_end = true;    //树结尾
}

图片名称

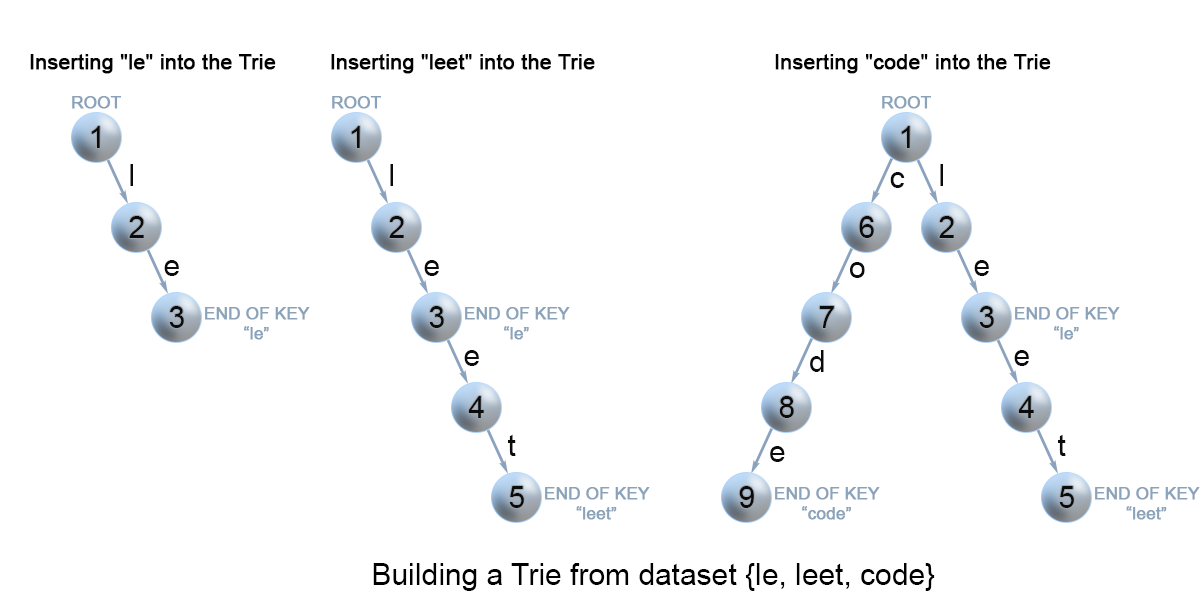
搜索键及前缀

每个键在 trie 中表示为从根到内部节点或叶的路径。我们用第一个键字符从根开始，。检查当前节点中与键字符对应的链接。有两种情况：

  • 存在链接。我们移动到该链接后面路径中的下一个节点，并继续搜索下一个键字符。

  • 不存在链接。若已无键字符，且当前结点标记为 isEnd，则返回 true。否则有两种可能，均返回 false :

    • 还有键字符剩余，但无法跟随 Trie 树的键路径，找不到键。
    • 没有键字符剩余，但当前结点没有标记为 isEnd。也就是说，待查找键只是Trie树中另一个键的前缀。
1
2
3
4
5
6
7
8
9
bool search(string word) {  
    Trie* node = this;
    for(const char& ch : word){
        int idx=ch-'a';
        if(node->children[idx] == nullptr) return false;
        node = node->children[idx];
    }
    return node->is_end;
}

搜索前缀与搜索键类似，只是不需要判断是否结尾，如果前缀能够完整在树中找到，那么直接返回true即可：

1
2
3
4
5
6
7
8
9
bool startsWith(string prefix) {
    Trie* node = this;
    for(const char& ch : prefix){
        int idx=ch-'a';
        if(node->children[idx] == nullptr) return false;
        node = node->children[idx];
    }
    return true;
}

字典树应用场景

字典树常用应用场景如下：

  • 自动补全
  • 拼写检查
  • IP路由
  • 打字预测等

字典树与哈希表对比

尽管哈希表可以在 $O(1)$ 时间内寻找键值，却无法高效的完成以下操作：

  • 找到具有同一前缀的全部键值
  • 按词典序枚举字符串的数据集

Trie 树优于哈希表的另一个理由是，随着哈希表大小增加，会出现大量的冲突，时间复杂度可能增加到$O(n)$，其中 $n$ 是插入的键的数量。与哈希表相比，Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 $O(m)$ 的时间复杂度，其中$m$为键长。而在平衡树中查找键值需要$O(m \log n)$ 时间复杂度。

参考文献

0%