排序

一去二三里，烟村四五家，亭台六七座，八九十枝花

基本排序算法

插入排序（稳定）

原理

将数组分为未排序的和已排序的两部分，在未排序的数组中依次读取新的元素，然后在已经排好序的数组中进行插入操作。关于插入排序更详细的描述请参考MIT课程中关于sort排序的讲解

性能

• 优点：已经排列好的数据不会被移动
• 缺点：插入动作可能导致大量元素的移动，平均时间复杂度为$O(n^2)$

实现

template <typename T>
void insert_sort(T data[], int n){
    for(int i=1,j;i<n;i++){    //令data[0]为第一个已经排好序的数组
        T temp = data[i];      //1到n-1则是未排序的数组，data[i]是还未排序的元素
        for(j = i; j>0 && temp < data[j-1]; j--)   //将data[i]依次与已排序数组中的元素对比，进行移动操作，temp < data[j-1]代表前面比后面大，位置不对
            data[j] = data[j-1];  //将元素依次移位，前面的大的挪到后面
        data[j] = temp;      //进行插入
    }
}

• 何时使用：当不需要额外空间，排序比较简单，当对连续的数据流进行排序时
• 何时不用：当平均情况很差时

选择排序（不稳定）

原理

找到数组中最小的元素，将其与第一个位置的元素交换，然后在剩余的data[1],……,data[n]中找到最小的元素，把他放到第二个位置。

性能

• 优点：赋值次数少
• 缺点：交换次数多

实现

template<typename T>
void select_sort(T data[], int n){
    for(int i=0,j,least; i < n-1; i++){
        for(j=i+1,least = i; j < n; j++){ //每次循环，least都等于i
            if(data[j] < data[least])
                least = j;   //least是最小元素的位置
        }
        if(i != least)
        	swap(data[least],data[i]);
    }
}

冒泡排序（稳定）

原理

不断交换相邻逆序元素实现排序

性能

• 优点：空间复杂度为$O(1)$
• 缺点：时间复杂度$O(n^2)$，做了大量无用比较

实现

template<typename T>
void bubble_sort(T data[], int n){
    for(int i = 0; i < n-1; ++i)
        for(int j = n-1; j > i; --j)
            if(data[j] < data[j-1])
                swap(data[j],data[j-1]);
}

高效排序算法

希尔排序（不稳定）

原理

实际上是一种改进的插入排序算法，将数组分为$h$个子数组，然后每一段进行排序，排序方法一般选择插入排序（考虑插入排序的优点，对几乎已经排好的数据可以达到线性操作）。

增量选择一般服从如下条件：

$$h_1=1\\ h_{i+1}=3h_i+1$$

当$h_{i+1}>n$时停止，希尔排序的原理可以用如下图进行表示：

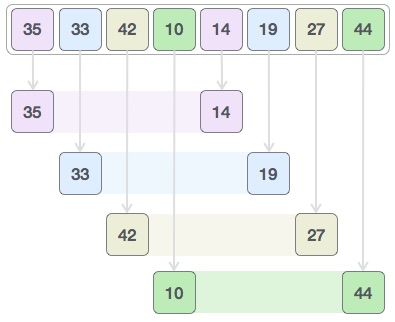
此处$h=4$，先对跨步长选取的子数组进行排序，排好序之后数列变为14 19 27 10 35 33 27 44，然后令$h=1$，再进行选择排序即可

性能

• 优点：降低了时间复杂度
• 缺点：不稳定，复杂度仍然较高

实现

template<typename T>
void shell_sort(T data[], int n){
    register int i,j,h_cnt,h;  //暗示程序会对这些变量进行频繁使用
    vector<int> increments{};
    for(h = 1; h < n; i++){
        increments.push_back(h);
        h = 3h + 1;
    }  //创建增量数组
    i--;
    //对增量进行循环
    for(; i >= 0; i--){
        h = increments[i];
        
        //划分增量子数组
        for(h_cnt = h; h_cnt < 2*h; h_cnt++){  //h_cnt = 2h 后，就开始重复了
            
            //对子数组进行插入排序
            for(j = h_cnt; j < n){   
                T tmp = data[j];
                k = j;
                while(k-h>0 && tmp < data[k-h]){  
                    data[k] = data[k-h];
                    k-=h;
                }
                data[k] = tmp;
                j += h;
            
            }
        }
    }
}

堆排序（不稳定）

原理

利用堆这种数据结构所设计的一种排序算法，堆本身是一个完全二叉树

性能

实现

void heapify(int arr[], int n, int i)     //创建堆，将堆的末端子节点作调整，使得子节点永远小于父节点
{ 
    //找到i的左右节点最大值，并与i进行交换
    int largest = i; // Initialize largest as root 
    int l = 2 * i + 1; // left = 2*i + 1      左节点
    int r = 2 * i + 2; // right = 2*i + 2     右节点
  
    // If left child is larger than root 
    if (l < n && arr[l] > arr[largest]) 
        largest = l; 
  
    // If right child is larger than largest so far 
    if (r < n && arr[r] > arr[largest]) 
        largest = r; 
  
    // If largest is not root 
    if (largest != i) { 
        swap(arr[i], arr[largest]); 
  
        // Recursively heapify the affected sub-tree 
        heapify(arr, n, largest);  
    } 
} 
  
// main function to do heap sort 
void heapSort(int arr[], int n) 
{ 
    // Build heap (rearrange array)  i從最後一個父節點開始調整
    for (int i = n / 2 - 1; i >= 0; i--) 
        heapify(arr, n, i);   
  
    // One by one extract an element from heap 相当于进行一个逆序过程，数组递增
    for (int i = n - 1; i >= 0; i--) { 
        // Move current root to end 
        swap(arr[0], arr[i]); 
  
        // call max heapify on the reduced heap 
        heapify(arr, i, 0); 
    } 
}

快速排序（不稳定）

原理

在排序时设置基准点，将小于基准点的数放置在左侧，大于的则放置在右侧，交换距离增大。快速排序本质上是一种基于二分法的递归排序方法，同时，快速排序还利用到了双指针。快速排序是不稳定的。

性能

• 优点：平均时间复杂度低（$O(NlogN)$）
• 缺点：如果数组中最小（大）的元素被选为边界点，那么时间复杂度为$O(n^2)$，不适合小数组

快速排序步骤：

1. 找到边界值（通常以数组中间值作为边界值）
2. 扫描数组，将数组中元素放入适当的子数组中

template<class T>
void quicksort(T data[], int first, int last){
    /*寻找边界值*/
    if(first < 0 || first >= data.size() || last < 0 || last >= data.size() || first > last) return;
    
    int lower = first + 1;  //双指针
    int upper = last;
    T bound = data[first];  //以第一个元素作为中间值
    
    /*进行排序操作*/
    while(lower <= upper){
        while(lower <= upper && data[lower] < bound) lower ++;   //这里存在隐患，如果最大的元素就是bound，lower会一直增长直到非正常中断，可以改为while(data[lower] < bound && lower < last)
        while(lower <= upper && data[upper] > bound) upper --;
        if(lower < upper) swap(data[lower++], data[upper--]);
        else lower ++; //结束循环的条件，也可以写upper--
    }
    /*交换边界值*/
    swap(data[first],data[upper]);   //first 此时作为分界点，需要被移动到合适的位置，即upper所在处
    
    /*递归*/
    if(first < upper - 1)
        quicksort(data,first,upper - 1);
    if(upper + 1 < last)
        quicksort(data, upper+1, last);
}

为了解决上述代码中的问题(如果数组中最小（大）的元素被选为边界点)，可以加入一段辅助代码

void quicksort(vector<int>& nums, int n){
    int i,max;
    if(n<2)
    return;
    for(i=1,max=0;i<n;i++){
    	if(nums[max]<nums[i])
    		max = i;
    }
    swap(nums[n-1],nums[max]);   //把最大值放在最后一个，防止最大值影响排序速度
    quicksort(nums,0,n-2);
}

常见应用

快速排序的思想在很多场合都可以借鉴，特别是在涉及数组元素移动的问题中。

一 LeetCode 283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

思路

我们可以设置快慢指针，慢指针指向0，快指针指向0后的第一个非0元素，然后交换快慢指针所指的值，然后递增慢指针。这里某个元素是否为0就可以视作快速排序中的基准值，代码如下：

void moveZeroes(vector<int>& nums) {
    int n = nums.size();
    int first = 0; //基准值
    for(int i=0;i < n;++i){
        if(nums[i] != 0){
            swap(nums[first], nums[i]);
            first++;
        }
    }
}

归并排序

原理

分而治之，对子数组进行排序，分治的思想也可以延续到许多问题中。

性能

• 优点：最好和最坏情况下时间复杂度相同，都是$O(n\text{log}n)$
• 缺点：合并数组需要额外空间

实现

// Merges two subarrays of arr[]. 
// First subarray is arr[l..m] 
// Second subarray is arr[m+1..r] 
void merge(int arr[], int l, int m, int r) 
{ 
    int i, j, k; 
    int n1 = m - l + 1;    //左子数组长度
    int n2 =  r - m; 
  
    /* create temp arrays */
    int L[n1], R[n2]; 
  
    /* Copy data to temp arrays L[] and R[] */
    for (i = 0; i < n1; i++) 
        L[i] = arr[l + i]; 
    for (j = 0; j < n2; j++) 
        R[j] = arr[m + 1+ j]; 
  
    /* Merge the temp arrays back into arr[l..r]*/
    i = 0; // Initial index of first subarray 
    j = 0; // Initial index of second subarray 
    k = l; // Initial index of merged subarray  
    while (i < n1 && j < n2)    //当两个数组都没有结束时
    { 
        if (L[i] <= R[j]) 
        { 
            arr[k] = L[i]; 
            i++; 
        } 
        else
        { 
            arr[k] = R[j]; 
            j++; 
        } 
        k++; 
    } 
  
    /* Copy the remaining elements of L[], if there 
       are any */
    while (i < n1) 
    { 
        arr[k] = L[i]; 
        i++; 
        k++; 
    } 
  
    /* Copy the remaining elements of R[], if there 
       are any */
    while (j < n2) 
    { 
        arr[k] = R[j]; 
        j++; 
        k++; 
    } 
} 
  
/* l is for left index and r is right index of the 
   sub-array of arr to be sorted */
void mergeSort(int arr[], int l, int r) 
{ 
    if (l < r) 
    { 
        // Same as (l+r)/2, but avoids overflow for 
        // large l and h 
        int m = l+(r-l)/2; 
  
        // Sort first and second halves 
        mergeSort(arr, l, m); 
        mergeSort(arr, m+1, r); 
  
        merge(arr, l, m, r);    //合并操作
    } 
}

归并排序原理上并不难理解，难的是如何实现相关代码，这里利用了递归的方式，空间复杂度是$O(n)$，如果想使空间复杂度为常数，可以使用自底向上的归并算法。

自底向上的归并算法，先两两排序合并，在44排序合并，直至结束，例如：[4,3,1,7,8,9,2,11,5,6]，其合并过程为¹：

step=1: (3->4)->(1->7)->(8->9)->(2->11)->(5->6)
step=2: (1->3->4->7)->(2->8->9->11)->(5->6)
step=4: (1->2->3->4->7->8->9->11)->5->6
step=8: (1->2->3->4->5->6->7->8->9->11)

实现：

见链表章节，使用归并排序对链表进行操作。

基数排序

单词的排序实际上就是基数排序，每一个字母表中包含了开头是相同字母的单词，然后再根据第二个字母，第三个字母这样依次划分下去。

实现

计数排序

原理

通过对数组中每个数字i出现的次数进行计数，将个数添加至count[i]中。

性能

• 优点：线性排序
• 缺点：如果数据偏差很大，可能导致空间开销非常大

自定义排序

在有些情况下，排序规则可能比较复杂，此时我们需要自定义排序规则，此处举一些例子总结自定义排序的写法。

字典序

31. 下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

C++ STL中有关于字典序排列的函数，用法如下：next_permutation(nums.begin(), nums.end());

排序算法复杂度分析

排序算法本质上可以转换一个决策树问题，根据决策树的深度可知，排序算法平均情况下最好的时间复杂度为$O(NlogN)$

参考文献

---

1. 1.排序链表 ↩