查找

Posted on | In ,

众里寻她千百度

常见查找算法

深度优先查找DFS（不撞南墙不回头）

基本模型

递归
1
2
3
4
5
6
7
8
void dfs(int step){
    //判断边界并返回，阶段二
    //如果有备忘录，那么此时可以返回备忘录中的值
    //尝试每一种可能 for(i=1;i<=n;i++){
        继续下一步 dfs(step+1)      //自上而下搜索
    }
    //返回  自下而上计算结果并返回
}
graph TB
    node("开始")
    judge1{"已遍历所有节点？"}
    node2("结束")
    dfs["进行深度优先搜索"]

    node-->judge1
    judge1-->|N|dfs
    dfs-->judge1
    judge1-->|Y|node2
迭代

深度优先搜索通常使用递归形式实现，如果要改为迭代形式，那么需要利用栈。

1
2
3
4
5
6
7
8
9
10
11
12
void dfs(int step){
    stack<int> search_set{}; // 在迭代实现中，我们采用栈保存当前待搜索对象
    search_set.push(first);  // 放入初始搜索点，例如树的根节点或数组的第一个节点或者图的初始任意节点
    while(!search_set.empty()) {  //搜索区间未空，就不能停止搜索
        int cur = search_set.top(); //获取当前搜索点
        search_set.pop();   
        
        visited[cur] = true;
        
        //添加和cur相关的新的搜索点，例如树的左子树、右子树，图的与当前节点相连的节点
    }
}

难点总结

理解dfs

在dfs中，每进行一次递归，就相当于深入一层。有些情况下可能会有不同路径，例如在迷宫类问题中，有上下左右四个方向，此时需要进行四次递归，相当于走了四条路径，构成了一个四叉树。

dfs思路

dfs分为两个阶段，在写dfs时要考虑清楚每个阶段的过程：

  • 自上而下搜索
  • 自下而上计算结果并返回
    • 在搜索的叶节点处直接返回叶节点值
    • 在非叶节点处根据下层计算结果与当前节点值进行计算

这里以leetcode120. 三角形最小路径和为例，对dfs思路进行整理。给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

1
2
3
4
5
6
7
8
9
10
11
12
13
int helper(vector<vector<int>>& triangle, int row, int col) {
    if (triangle.size() - 1 == row) {  //到达最后一行, 在搜索的叶节点处直接返回叶节点值
        return triangle[row][col];
    }

    int down = helper(triangle, row + 1, col);   //自上而下搜索
    int right = helper(triangle, row + 1, col + 1);

    return min(down, right) + triangle[row][col];    //在非叶节点处根据下层计算结果与当前节点值进行计算
}
int minimumTotal(vector<vector<int>>& triangle) {
    return helper(triangle, 0, 0);
}
搜索入口

为了保证搜索覆盖的全面性，我们需要对所有的待搜索的点进行搜索，例如我们对一个有$n$个节点的图进行搜索，代码框架如下：

1
2
3
4
5
for (int i = 0; i < n; ++i) {
    if (!visited[i]) {
        dfs(i);
    }
}

即使图中有不相连的部分，因为我们经过了遍历，所以深度优先搜索能保证所有的节点都访问到。

边界判断

边界判断是DFS的重要部分，保证了DFS能够顺利退出递归，以下总结一些常见的DFS退出条件。首先，由于DFS是递归算法，所以很可能会搜索到重复的位置，因此往往需要一个visited向量，用于保存已经访问的位置，如果已经visited，那么直接返回。

  1. 指针类DFS

多见于处理链表或二叉树问题的DFS中，常见退出条件如下：

  • head == nullptr：return head;
  • visited(head) == true：return head;
  1. 数组类DFS

常见退出条件如下：

  • 范围超过数组边界：if(cur_m < 0 || cur_n < 0 ||cur_m >= m || cur_n >= n)
  • 已经访问过指定位置：if(visited[cur_m][cur_n] == 1)
  • 所在位置不满足搜索要求：if(int_to_sum(cur_m) + int_to_sum(cur_n) != k)
  • 给定数组搜索范围[left,right)（左开右闭区间），那么搜索结束的标志为left == right，见leetcode从前序与中序遍历序列构造二叉树
返回值

递归由于涉及到多次函数调用，因此返回值的计算可能会比较麻烦，这里针对dfs给出一个比较套路化的返回规则，首先，如果不满足条件，那么就在进入递归函数后立刻返回；其次，最终的返回值应当放在递归函数结尾给出。

1
2
3
4
5
6
7
8
int traverse(TreeNode* root){
    if(root==nullptr )    //第一返回位置，不满足条件，直接返回
        return 0;
    int left=traverse(root->left);
    int right=traverse(root->right);
    tilt+=Math.abs(left-right);
    return left+right+root->val;  //第二返回位置，在递归体结束后返回
}
何时增加深度

当明确有一条搜索路径时，我们再去增加递归深度，例如在二叉树搜索中，如果我们明确了某个子节点不为空，再向这条子节点进行搜索，这样可以减少递归深度，提高效率：

1
2
3
4
5
6
7
8
if(root->left!=nullptr){ //左节点存在时，再进行深度搜索哦
    dfs(root->left, temp, ans); 
    if(temp.back() == '>')temp.pop_back();

    while(temp.back() != '>'){
        temp.pop_back();
    }
}
被搜索节点的状态

在深度优先搜索中，一个被搜索节点一般有三个状态：

  • 未搜索：该节点尚未被搜索
  • 搜索中：我们正在搜索该节点和相邻的节点，但是该节点相邻的节点还未搜索完成
  • 已完成：我们搜索过所有的相邻节点，回溯了该节点，搜索已完成
剪枝

在某些情况下，我们需要剪枝操作，例如当前位置和前一个位置相同，那么我们直接跳过该步骤即可，剪枝的操作代码如下：

1
if(i != start && s[i] == s[i-1]) continue;  //去除重复

将上述语句放入dfs的for循环中，即可实现剪枝操作。

常见DFS类型总结及模板

判断搜索路径是否存在

此类问题要求我们判断搜索树中是否存在一条符合条件的搜索路径，因此搜索过程中，一旦找到了路径，我们应当立刻返回，以免不必要的递归造成效率的降低。这里以面试题 04.01. 节点间通路为例，对此类问题模板进行总结。

思路

我们希望找到答案后直接返回，而找到答案的可能性有两种，一种是在本层中直接找到答案；另一种是在深层递归中找到答案。因此我们需要进行两次判断，当在本层中找到答案后直接返回；当在下层搜索后，判断是否找到答案，然后根据情况中断搜索，模板如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool search(int start,int target){
    visited[start] = 1;
    bool result = false;                    
    for(...){
        int cur_pos = adList[start][i];
        
        if (viewed[cur_pos]==0){         //对没有搜索的点处理
            if(cur_pos==target){         //找到后直接返回
                return true;
            }
            result = search(cur_pos,target);   //递归搜索
            
            if(result == true)                 //找到后中断搜索
                break;
        }
        
    }
    return result;
}

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool search(int start,int target){
    viewed[start] = 1;
    bool result = false;                    
    for(int i=1;i<adList[start].size();i++){
        int cur_pos = adList[start][i];     //循环遍历所有分支
        
        if (viewed[cur_pos]==0){         //对没有搜索的点处理
            if(cur_pos==target){         //找到后直接返回
                return true;
            }
            result = search(cur_pos,target);   //递归搜索
            if(result == true)                 //找到后中断搜索
                break;
        }
        
    }
    return result;
}

从上面的代码中我们可以看到，此时判断是否退出的条件放在了循环体中，意味着我们找到答案后会立刻退出，另外递归后也加了一条判断语句，确保找到答案立刻退出。

获取累加值

有些dfs问题需要我们记录累加值，这种情况下，我们需要在dfs开始时设置一个临时变量，然后结尾处返回该临时变量，每个递归函数都会定义自己的局部变量，而第一次递归时定义的局部变量即为最终的计算结果。一个框架如下所示：

1
2
3
4
5
6
7
8
9
10
int dfs(int depth){
    int ans = 0;
    if(...){ //递归结束条件
        return ...; //返回边界值
    }
    for(...){ //遍历当前搜索集合
        ans += dfs(depth+1);   //遍历搜索树的每一个节点
    }
    return ans;
}
计算递归深度

在有些情况下，我们需要计算递归树的深度，例如计算二叉树的深度，其代码如下：

1
2
3
4
5
6
7
8
int maxDepth(TreeNode* root) {
    if(root == NULL) return 0;
    int depth = 0;
    // 关键语句，我们遍历了所有可行分支，对于二叉树来说，一共有两个分支，然后获得其中的最大深度
    depth = max(maxDepth(root->left), maxDepth(root->right));
    // 返回值需要+1，因为计算深度时要包含当前节点
    return depth+1;   
}

以此类推，我们可以延伸到计算任意递归函数的深度，只需要循环遍历所有分支，找到分支最大深度即可。例如leetcode364. 加权嵌套序列和 II，计算递归深度的代码如下：

1
2
3
4
5
6
7
8
9
10
11
int getSum(vector<NestedInteger>& nestedList, int depth){
    int sum = 0;
    for(auto ni : nestedList){
        if(ni.isInteger()){
            sum += depth * ni.getInteger();
        }else{
            sum += getSum(ni.getList(), depth - 1);
        }
    }
    return sum;
}
获得所有可能解的DFS

例题

301. 删除无效的括号

删除最小数量的无效括号，使得输入的字符串有效，返回所有可能的结果。说明: 输入可能包含了除 ( 和 ) 以外的字符。

思路

这个问题可以划分为三个子问题：

  • 判断括号是否合法
  • 计算有多少个左右括号需要删除
  • 递归删除括号，得到结果后进行保存

前两个子问题我们可以通过栈实现，后一个可以通过DFS实现 ，重点是第三个问题，第三个问题中，我们又可以列举出如下几个问题：

  • 先删除哪种括号？先删除右括号，如果先删除左括号，可能导致前缀非法，例如对于())(，如果我们先删除了第一个左括号，那么会变成))(，原来合法的前缀反而不合法了。这样会构成额外的枝。
  • 如何避免重复解 ，例如对于(()，删掉第一个和第二个左括号，得到的结果都为()，所以我们需要剪枝操作

例子

我们以s = ")())("为例，需要删除两个右括号，一个左括号，那么我们的递归函数为dfs(s, l=1, r=2)，删除过程的递归树如下：

graph TB
    node["dfs( s = )())( , l=1, r=2)"]
    node1["dfs(s = *())( , l=1, r=1)"]
    node2["dfs(s = )(*)( , l=1, r=1)"]
    node3["dfs(s = )()*( , l=1, r=2)"]
    node4["dfs(s = *(*)( , l=1, r=0)"]
    node5["dfs(s = *(*)* , l=0, r=0): 合法"]
    node6["dfs(s = )(**( , l=1, r=0)"]
    node7["dfs(s = )(*** , l=0, r=0): 非法"]

    node---node1
    node---node2
    node--冗余枝条---node3
    node1---node4
    node4---node5
    node2---node6
    node6---node7

可以看出递归深度为$l+r$，所以时间复杂度为$2^{l+r}$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
bool isValid(const string& s){
    int count = 0;
    for(const char ch : s){
        if(ch == '(') ++count;
        if(ch == ')') --count;
        if(count < 0) return false; //小于0说明右括号落单，一定是非法
    }
    return count == 0;
}
vector<string> removeInvalidParentheses(const string& s){
    int l=0;
    int r=0;
    
    /*
    **    计算最少需要的左括号和右括号的值，这里没有用栈的方法，而是
    **    使用了投票法
    */
    for(const char ch : s){
        l += (ch == '(');
        if(l == 0)                 //表示右括号会落单，因此如果l==0，如果出现右括号，一定删除
            r += (ch == ')');
        else
            l -= (ch == ')');
    }
    vector<string> ans;
    dfs(s, 0, l, r, ans);
    return ans;
}

/*-----------------------------------------------------------
*    dfs -- 递归进行括号删除                                  
*                                                           
*    INPUT: s     -- 待处理字符串                   
*           start -- 上一次删除的括号的位置，每次删除从该位置之后开始
*           l     -- 剩余待删除左括号数目
*           r     -- 剩余待删除右括号数目
*           ans   -- 答案
*-----------------------------------------------------------*/
void dfs(const string& s, int start, int l, int r, vector<string>& ans){
    if(l == 0 && r == 0){
        if(isValid(s)) ans.push_back(s);
        return;
    }
    
    for(int i=start; i<s.size(); i++){
        if(i != start && s[i] == s[i-1]) continue;  //去除重复
        
        if(s[i] == '(' || s[i] == ')'){
            string curr = s;
            curr.erase(i, 1);
            if(r > 0 && s[i] == ')') dfs(curr, i, l, r-1, ans);    //优先删除右括号
            else if(l > 0 && s[i] == '(') dfs(curr, i, l-1, r, ans);
        }
    }
}

DFS优化

动态规划与DFS结合

在深度优先搜索中，可能会产生大量重复计算，如果我们能像动态规划那样，牺牲一些空间来保存中间结果，能够有效减少计算时间，DFS与DP结合的代码框架如下，其中有两个关键步骤，记录与提取：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int helper(vector<vector<int>>& board, 
           vector<vector<int>>& mem, 
           int row, 
           int col) {
    if (board.size() - 1 == row) {
        return board[row][col];
    }
    if (mem[row][col]) return mem[row][col];            //返回备忘录中的值

    int down = helper(board, mem, row + 1, col);        //向下向右搜索
    int right = helper(board, mem, row, col + 1);

    int ans = min(down, right) + board[row][col];
    mem[row][col] = ans;                                //记录备忘录中的值
    return ans;
}

329. 矩阵中的最长递增路径

给定一个整数矩阵，找出最长递增路径的长度。对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外（即不允许环绕）。

1
2
3
4
5
6
7
8
9
10
示例 1:

输入: nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
输出: 4 
解释: 最长递增路径为 [1, 2, 6, 9]。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
public:
    int r = 0;        // Row num of matrix
    int c = 0;        // Column num of matrix
    
    /*
    **    Moving directions
    */
    vector<int> dx = {1,-1,0, 0};
    vector<int> dy = {0, 0,1,-1};
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        /*
        **    Init work
        */
        if(matrix.empty()) return 0;
        r = matrix.size();
        c = matrix[0].size();
        int ans = 0;
        /*
        **    This dp vector stores the mid results to avoid duplicate calculation
        **    dp[i][j] means the longest pathes length which is end at (i,j)
        */
        vector<vector<int>> dp(r, vector<int>(c,0));   
                                                   
        /*
        **    Search at each element of the matrix
        */
        for(int i=0;i<r;i++){
            for(int j=0;j<c;j++){
                ans = max(ans,dfs(matrix, i, j, dp));
            }
        }
        return ans;
    }

    /*----------------------------------------------------------
    *  dfs -- Find all the possible pathes of the matrix
    *
    *  INPUT:  matrix -- The matrix which needs to be searched
    *          cur_r  -- Current row in the matrix
    *          cur_c  -- Current col in the matrix
    *          dp     -- The matrix which store mid results
    *  OUTPUT: The longest pathes of current search position
    *          ended at (cur_r, cur_c)
    *----------------------------------------------------------*/
    int  dfs(vector<vector<int>>& matrix, int cur_r, int cur_c, 
             vector<vector<int>>& dp){
        /*
        **    Return if dp[cur_r][cur_c] != 0 which means the result 
        **    at position (cur_r, cur_c) has already been calculated
        */
        if(dp[cur_r][cur_c] != 0) return dp[cur_r][cur_c];

        for(int i=0;i<4;i++){
            int nr = cur_r + dx[i], nc = cur_c + dy[i];    // New row and col
            /*
            **    Only if the adjcent is valid then apply dfs
            */
            if(nr >= 0 && nr < r && nc >= 0 && nc < c && matrix[nr][nc] < matrix[cur_r][cur_c])   
                dp[cur_r][cur_c] = max(dp[cur_r][cur_c],dfs(matrix, nr, nc, dp));
        }
        return ++dp[cur_r][cur_c];
    }
};

广度优先搜索BFS

特点

广度优先搜索能够保证在搜索到d+1距离的位置时，距离为d的位置都已经搜索过，所以可以使用广度优先搜索处理例如迷宫中最短路径等问题。

实现

  • 创建队列保存搜索点
  • 保存初始搜索点
  • 弹出搜索点，并以搜索点为基准，遍历所有搜索分支，例如在迷宫当中，有上下左右四个方向，即四个搜索分支
  • 每个搜索分支下，添加新的搜索点，扩大搜索范围

基本模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//广度优先通常采用迭代形式
void BFS(...){
    //判断是否返回
    //初始化
    queue<int> res{};
    res.push(root->val);    
    
    //bfs 循环
    while(!res.empty()){
        //新建vector<int> temp 用于保存每一层的结果
        int width = res.size();  //保存当前层长度
        //当前层循环打印
        for(int i=0;i<width;i++){
            //1. 出队列
            //2. 访问
            //3. 入队列  将待搜索的位置放入队列中
        }
        //将temp添加至res
    }
    //返回
}

广度优先搜索一般要利用队列，来实现对于一层的存储。

难点及要点总结

广度优先过程中会出现重复搜索的问题，即相邻两个待搜索对象，第一个时刻由对象1搜索到了对象2，第二个时刻又由对象2搜索到了对象1，解决方法是使用visited矩阵或集合进行标记，已经搜索过的就直接跳过。

DFS与BFS的比较

这张图直观地对DFS与BFS进行了比较：

图片名称

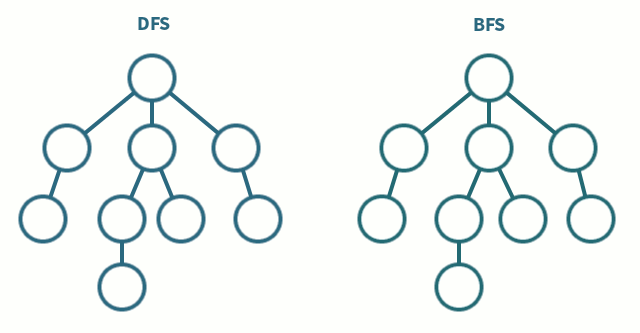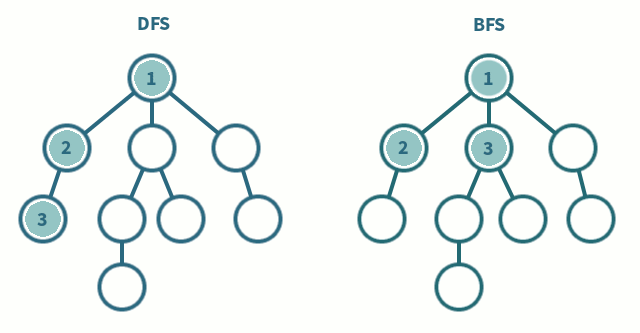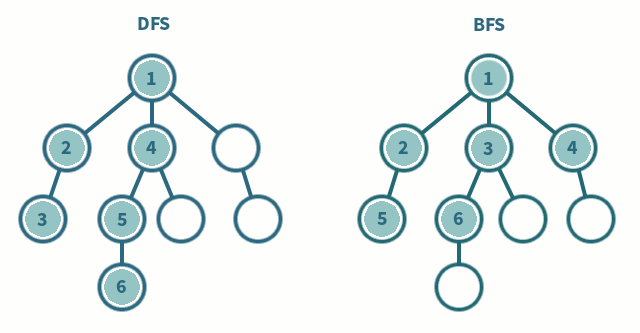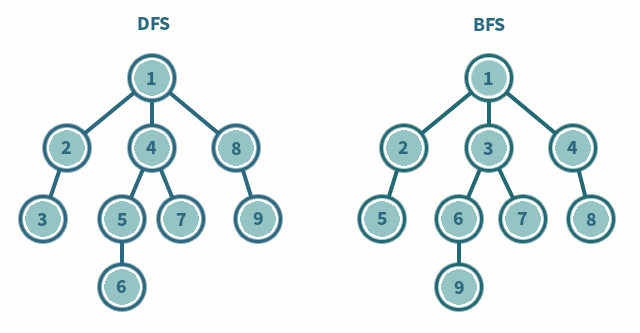
专题：图的DFS和BFS搜索

DFS搜索

1
2
3
4
5
6
7
8
9
//在图中搜索所有为'O'的格子，然后将格子置为'#'
void dfs(vector<vector<char>>& board, int i, int j, int m, int n){
    if(i < 0 || j < 0 || i >= m || j >= n || board[i][j] == 'X' || board[i][j] == '#') return; //不满足搜索结果
    board[i][j] = '#';
    dfs(board, i+1, j, m,n);
    dfs(board, i-1, j, m,n);
    dfs(board, i, j+1, m,n);
    dfs(board, i, j-1, m,n);
}

BFS搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Queue<int[]> q = new LinkedList<>();
for (int row = 0; row < m; row++) {
    for (int col = 0; col < n; col++) {
        if (rooms[row][col] == GATE) {
            q.add(new int[] { row, col });   //将所有搜索点放入队列中
        }
    }
}
while (!q.isEmpty()) {
    int[] point = q.poll();
    int row = point[0];
    int col = point[1];
    for (int[] direction : DIRECTIONS) {
        int r = row + direction[0];     //下一个搜索位置
        int c = col + direction[1];   
        if (r < 0 || c < 0 || r >= m || c >= n || rooms[r][c] != EMPTY) {
            continue;   
        }
        rooms[r][c] = rooms[row][col] + 1;   
        q.add(new int[] { r, c });
    }
}

如果用画图的形式解释BFS在图中的搜索，那么其形式如下：

1
2
3
4
5
6
7
8
9
//以传染病模型为例，其中1是被感染的人，一开始他会将上下左右四个方向上的人全部感染，产生四个新感染的人，即四个新的搜索点
0 0 0 0 0       0 1 0 0 0       0 1 0 0 0        0 1 0 0 0         0 1 0 0 0
0 1 0 0 0       0 1 0 0 0       0 1 1 0 0        0 1 1 0 0         1 1 1 0 0
0 0 0 0 0       0 0 0 0 0       0 0 0 0 0        0 1 0 0 0         0 1 0 0 0
0 0 0 0 0       0 0 0 0 0       0 0 0 0 0        0 0 0 0 0         0 0 0 0 0

这四个新的搜索点会继续扩散，直到所有的人都感染为止。所以BFS类似于一种传染病模型，会将临近的单位全部感染

那么问题来了，当BFS有不只一个搜索点，例如在传染病模型中，有多个初始病人，那么我们如何知道新病人是由哪个病人感染的呢？这个问题不必担心，由于BFS是一种临近搜索，因此新病人必然是由离得最近的病人感染的，BFS的特性能够保证传播符合实际情况，不会出现病人被离得远的病人所感染。

专题：岛屿问题

岛屿问题是经典的二维搜索问题，本节将对常见的岛屿问题进行总结。

求连通域数目

  1. leetcode 695

求4-连通域最大面积，这个问题很经典，需要记住代码

1
2
3
4
5
6
7
8
9
10
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]
 
 返回6

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int area(int r, int c, vector<vector<int>>& grid){
        if(r < 0 || r >= grid.size() || c < 0 || c >= grid[0].size() 
          || grid[r][c] == 0) return 0;    //查找到某一块边界点，停止
        grid[r][c] = 0;   //防止重复查找，也可以通过设置一个flag矩阵，保存已经查找过的区域
        return (1 + area(r+1,c,grid)+area(r-1,c,grid)+area(r,c+1,grid)+area(r,c-1,grid));  //一直查找直到达到边界点
    }
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        if(grid.size() == 0 || grid[0].size() == 0) return 0;
        int ans = 0;
        for(int r = 0;r<grid.size();r++){
            for(int c = 0;c<grid[0].size();c++){    //遍历岛屿的每一个格子
                int temp = area(r,c,grid);    //一次执行过程中，area函数就会将相邻的连通区域全部置零，如果需要统计连通域个数，那么设置一个标记位进行统计即可。
                ans = max(ans,temp);
            }
        }
        return ans;
    }
};

130. 被围绕的区域搜索
给定一个二维的矩阵，包含 ‘X’ 和 ‘O’（字母 O）。找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

1
2
3
4
X X X X
X O O X
X X O X
X O X X

运行函数后，矩阵变为：

1
2
3
4
X X X X
X X X X
X X X X
X O X X

思路

如果我们认为O所在位置为海岛，那么该问题的本质就是求所有与边界不联通的海岛的位置，然后进行替换。所以我们应当从边界位置处的海岛O开始搜索，找到所有的和边界相连的海岛，那么剩下的海岛就一定是被X包围的。

任务

  • 找到边界岛屿
  • 从找到的边界岛屿处开始搜索（每一个边界岛屿都要作为搜索的起始点）
  • 搜索过程中，将与边界相连的海岛替换为#（方便后续恢复）
  • 遍历棋盘，将不与边界相连的海岛淹没，将与边界相连的海岛恢复

代码

解法1：深度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    void solve(vector<vector<char>>& board) {
        if(board.size() == 0 || board[0].size() == 0) return;
        int m = board.size(), n = board[0].size();
        for(int i=0;i < m;i++){
            for(int j=0;j < n;j++){
                bool isEdge = (i == 0 || j == 0 || i == m-1 || j == n-1);
                if(isEdge && board[i][j] == 'O'){
                    dfs(board, i, j,m,n);
                }
            }
        }

        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(board[i][j] == 'O') board[i][j] = 'X';
                else if(board[i][j] == '#') board[i][j] = 'O';
            }
        }
    }

    void dfs(vector<vector<char>>& board, int i, int j, int m, int n){
        if(i < 0 || j < 0 || i >= m || j >= n || board[i][j] == 'X' || board[i][j] == '#') return;
        board[i][j] = '#';
        dfs(board, i+1, j, m,n);
        dfs(board, i-1, j, m,n);
        dfs(board, i, j+1, m,n);
        dfs(board, i, j-1, m,n);
    }
};

200. 岛屿数量

专题：迷宫问题

迷宫问题中，我们可能遇到有效路径、遍历迷宫以及最短路径等问题，本节将针对常见的迷宫问题进行总结

寻找迷宫中的门

你被给定一个 m × n 的二维网格，网格中有以下三种可能的初始化值：

  1. -1 表示墙或是障碍物
  2. 0 表示一扇门
  3. INF 无限表示一个空的房间。然后，我们用 231 - 1 = 2147483647 代表 INF。你可以认为通往门的距离总是小于 2147483647 的。

你要给每个空房间位上填上该房间到 最近 门的距离，如果无法到达门，则填 INF 即可。

例如，给定迷宫

1
2
3
4
5
>INF  -1  0  INF
>INF INF INF  -1
>INF  -1 INF  -1
>  0  -1 INF INF
>

>

输出为：

1
2
3
4
5
>  3  -1   0   1
>  2   2   1  -1
>  1  -1   2  -1
>  0  -1   3   4
>

思路

从门使用BFS进行搜索，能够以扩散传播的方式，对周边区域进行搜索，从而确保周围的房间能够到达最近的门

任务

  • 找到门坐标
  • 从门坐标开始，进行深度优先搜索

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void wallsAndGates(vector<vector<int>>& rooms) {
    if(rooms.size() == 0 || rooms[0].size() == 0) return;
    int m = rooms.size();
    int n = rooms[0].size();

    vector<vector<int>> direction{{0,-1}, {0,1}, {1,0}, {-1,0}};
    queue<vector<int>> point_queue{};

    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(rooms[i][j] == 0) point_queue.push(vector<int>{i,j});
        }
    }
    while(!point_queue.empty()){

        auto p = point_queue.front();
        point_queue.pop();

        for(int i=0;i<direction.size();i++){
            int r = p[0] + direction[i][0];
            int c = p[1] + direction[i][1];
            if(r < 0 || c < 0 || r >= m || c >= n || rooms[r][c] != 2147483647) continue;
            rooms[r][c] = rooms[p[0]][p[1]] + 1;
            point_queue.push(vector<int>{r,c});
        }

    }
}

判断是否能走到终点

迷宫三问

490. 迷宫

505. 迷宫 II

迷宫II是对迷宫I的问题的延伸，我们不仅要判断能否到达终点，还要记录从起点到终点的最短路径。这里我们定义了一个distance矩阵，把每一个可以到达的方块距离起点的最短距离记录下来，然后返回目标点所在的值即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

public class Solution {
    public int shortestDistance(int[][] maze, int[] start, int[] dest) {
        int[][] distance = new int[maze.length][maze[0].length];
        for (int[] row: distance)
            Arrays.fill(row, Integer.MAX_VALUE);
        distance[start[0]][start[1]] = 0;
        dfs(maze, start, distance);
        return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];
    }

    public void dfs(int[][] maze, int[] start, int[][] distance) {
        int[][] dirs={{0,1}, {0,-1}, {-1,0}, {1,0}};
        for (int[] dir: dirs) {
            int x = start[0] + dir[0];
            int y = start[1] + dir[1];
            int count = 0;
            while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {
                x += dir[0];
                y += dir[1];
                count++;
            }
            x = x-dir[0]; y = y-dir[1];
            // 注意！上面的循环结束时，实际上走到了非法区域，需要后退一步，才能走到正确的位置，所以需要x = x-dir[0]; y = y-dir[1];
            if (distance[start[0]][start[1]] + count < distance[x][y]) {    
                distance[x][y] = distance[start[0]][start[1]] + count;
                dfs(maze, new int[]{x,y}, distance);
            }
        }
    }
}

迷宫遍历

有些问题需要我们遍历迷宫中所有可以行走的路径，例如489. 扫地机器人

房间（用格栅表示）中有一个扫地机器人。格栅中的每一个格子有空和障碍物两种可能。扫地机器人提供4个API，可以向前进，向左转或者向右转。每次转弯90度。当扫地机器人试图进入障碍物格子时，它的碰撞传感器会探测出障碍物，使它停留在原地。请利用提供的4个API编写让机器人清理整个房间的算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
interface Robot {
  // 若下一个方格为空，则返回true，并移动至该方格
  // 若下一个方格为障碍物，则返回false，并停留在原地
  boolean move();

  // 在调用turnLeft/turnRight后机器人会停留在原位置
  // 每次转弯90度
  void turnLeft();
  void turnRight();

  // 清理所在方格
  void clean();
}

思路

由于我们不清楚起始位置在哪里，因此只能使用相对信息对位置坐标进行记录，令起始点坐标为(0,0)，然后实施dfs

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class Pair<F, S> {
    public F first;
    public S second;

    public Pair(F first, S second) {
        this.first = first;
        this.second = second;
    }

    @Override
    public boolean equals(Object o) {
        Pair<F, S> p = (Pair<F, S>) o;
        return Objects.equals(p.first, first) && Objects.equals(p.second, second);
    }

    @Override
    public int hashCode() {
        return first.hashCode() ^ second.hashCode();
    }
}

class Solution {
    // going clockwise : 0: 'up', 1: 'right', 2: 'down', 3: 'left'
    int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    Set<Pair<Integer, Integer>> visited = new HashSet();
    Robot robot;

    public void goBack() {
        robot.turnRight();
        robot.turnRight();
        robot.move();
        robot.turnRight();
        robot.turnRight();
    }

    public void backtrack(int row, int col, int d) {
        visited.add(new Pair(row, col));
        robot.clean();
        // going clockwise : 0: 'up', 1: 'right', 2: 'down', 3: 'left'
        for (int i = 0; i < 4; ++i) {
            int newD = (d + i) % 4;
            int newRow = row + directions[newD][0];
            int newCol = col + directions[newD][1];
            // 当下一个点未访问过并且可以到达时，再进行dfs
            if (!visited.contains(new Pair(newRow, newCol)) && robot.move()) {
                backtrack(newRow, newCol, newD);
                goBack();
            }
            // turn the robot following chosen direction : clockwise
            robot.turnRight();
        }
    }

    public void cleanRoom(Robot robot) {
        this.robot = robot;
        backtrack(0, 0, 0);
    }
}

二分查找（常常和二叉树一起出现）

基本原理

每一次循环都能排除掉一半以上的元素，最后把区间限定在一个元素，二分查找要求被查找的对象必须经过排序。循环条件为left < right，如果被查找元素未经排序，那么循环条件可能发生改变，例如LeetCode154旋转数组。

算法要求

  1. 必须采用顺序存储结构
  2. 必须按照关键字大小有序排列

算法适用场景及每个场景对应框架(重要！)

二分查找最适用的场景包括三个：寻找一个数、寻找左侧边界、寻找右侧边界。大部分涉及寻找特定值$x$的问题，都可以使用二分查找进行解决，例如寻找一个数的整数开方问题等。

二分查找基本框架2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = ...;           //right的值为查找的右边界（搜索结果包括右边界）
                                         //对于本题，就是nums.size()-1
    //搜索区间为][left,right]，左闭右闭
    while(left < right) {  //结束时 left == right 留下的搜索区间为[left,right];
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {    //使用else if显示所有情况
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;    //这里需要对nums[left]进行单独判断
}
寻找一个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int binary_search(vector<int>& nums, int target) {
    int left = 0, right = nums.length - 1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;       
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}
寻找左侧边界的二分查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int left_bound(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] >= target) { //即使找到也不能停止，要不断压缩右边界，确保找到的一定是左边界
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况，这个程序也可以用来搜索第一个大于target的位置（如果nums[left]!=target）
    if (left >= nums.length || nums[left] != target)  
        return -1;
    return left;
}
寻找右侧边界的二分查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] <= target) {
            left = mid + 1;  //收缩左侧边界
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

算法要点及难点

本节将对二分查找的一些难点及要点进行总结。

二维矩阵中的二分查找

有些情况下，我们需要对二维矩阵进行二分查找的操作，如果我们按照先分行再分列的方法，搜索效率很低，因此我们采用整体搜索法，假设矩阵大小为$m×n$，那么待搜索的元素的个数为$m×n$，所以left = 0, right = m*n-1，在矩阵中进行二分查找的框架如下所示，时间复杂度为$O(log(mn))$：

1
2
3
4
5
6
7
8
9
10
11
int left = 0, right = m * n - 1;
int pivotIdx, pivotElement;
while (left <= right) {
    pivotIdx = (left + right) / 2;
    pivotElement = matrix[pivotIdx / n][pivotIdx % n];   // 关键，行为当前索引p/n，列为p%n
    if (target == pivotElement) return true;
    else {
        if (target < pivotElement) right = pivotIdx - 1;
        else left = pivotIdx + 1;
    }
}

算法讲解

注：以下内容在难以判断循环结束后left是否为搜索位置时较为好用

  1. 取中位数索引

二分法第一个麻烦的问题就是对中位数索引的判断，如果按照如下方式写，可能发生越界情况：

1
int mid = (left + right)/2;

所以可以写为：

1
int mid = left + (right - left)/2;

一个更好的写法是：

1
int mid = unsigned(left+right)>>2;

中位数的处理方法

根据元素个数为奇数还是偶数，中位数的选取也会比较麻烦，当元素个数为偶数时，有左右中位数的区分

  • 当数组的元素个数是偶数的时候：

使用 int mid = unsigned(left + right) >> 1 得到左中位数的索引；

使用int mid = unsigned(left + right + 1) >> 1得到右中位数的索引。

  1. 边界选取

左右边界选取时要注意，如果左右边界不包括目标数值，会导致错误，例如LeetCode 第 35 题：“搜索插入位置” ，当 target 比数组中的最后一个数字还要大（不能等于）的时候，插入元素的位置就是数组的最后一个位置 + 1，即 (len - 1 + 1 ) = len，如果忽略掉这一点，把右边界定为 len - 1 ，代码就不能通过在线测评1。所以left = 0，right = len而不是len-1。

  1. 循环条件

循环条件一般可以写为：left < right，当循环结束时，一定有left == right，返回left或者right都可以，但是，退出循环的时候遗漏了一个元素没有看，那就是left或right索引上的值。

  1. 分支逻辑编写

二分法的分支逻辑很简单，这里有一个关键是，在分支逻辑中，一个分支是包括中位数的，另一个是排除中位数的。根据上面的分支逻辑的分析，那么会有两种情况出现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/******1******/
if(排除中位数的逻辑分支){
    left = mid+1;  //目标元素至少是中位数，但不包括中位数
}
else{
    right = mid;  //目标元素至多是中位数，且包括中位数
}

/******2******/
if(排除中位数的逻辑分支){
    right = mid-1;  //目标元素至多是中位数，但不包括中位数
}
else{
    left = mid;  //目标元素至少是中位数，且包括中位数
}
  1. 根据分支逻辑选择左右中位数，选择标准是避免死循环

死循环容易发生在区间只有两个元素的时候

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/*下面的代码中，如果只有两个元素，一旦进入左边界，那么左边界不收缩，如此下去会进入死循环，因此需要换成右中位数*/
int mid = unsigned(left + right) >> 1;

if(排除中位数的逻辑分支){
    right = mid-1;  //目标元素至多是中位数，但不包括中位数
}
else{
    left = mid;  //目标元素至少是中位数，且包括中位数
}

/*一样的道理，下面的也需要换成左中位数*/ 
int mid = unsigned(left + right + 1) >> 1;

if(排除中位数的逻辑分支){
    left = mid+1;  //目标元素至多是中位数，但不包括中位数
}
else{
    right = mid;  //目标元素至少是中位数，且包括中位数
}
  1. 后处理

当退出循环后，我们可能需要对两边夹逼剩下的那个数做一个单独的处理，何时要进行后处理呢：

  • 如果你的业务逻辑保证了你要找的数一定在左边界和右边界所表示的区间里出现，那么可以放心地返回 left 或者 right，无需再做判断；

  • 如果你的业务逻辑不能保证你要找的数一定在左边界和右边界所表示的区间里出现，那么只要在退出循环以后，再针对 nums[left] 或者 nums[right] （此时 nums[left] == nums[right]）单独作一次判断，看它是不是你要找的数即可，这一步操作常常叫做“后处理”。

例如

LeetCode 第 704 题：二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

分析：因为目标数有可能不在数组中，当候选区间夹逼成一个数的时候，要单独判断一下这个数是不是目标数，如果不是，返回 -1。

模板(来自例题1)

二分查找的一个难点主要是边界条件的控制，如果控制不好，可能会陷入死循环当中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int findDuplicate(vector<int> &nums) {
    int len = nums.size();     
    int left = 0;
    int right = len - 1; 

    while (left < right) {
        int mid = unsigned int(left + right + 1) >> 1;   
        int counter = 0;
        for (int num:nums) {
            if (num < mid) { 
                counter++;
            }
        }

        if (counter >= mid) {   //小数较多
            right = mid - 1;        //收缩右边界
        } else {             //大数较多
            left = mid;
        }
    }
    return left;
}

说了这么多，总结一下常用模板

1
2
3
4
5
6
while(left < right){
    long long mid = left + ((right-left)>>1);   //左中位数
    if(target > mid) left = mid + 1;            //排除中位数的逻辑分支，left++
    else right = mid;                           //包含中位数的逻辑分支，right保持不变
} 
return left;

例题

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

1
2
输入: [1,3,4,2,2]
输出: 2

思路：使用二分查找的方式，把1～n个数字从中间数m分为两部分，统计每个区间中数字的个数，如果某个区间数字个数大于m，那么一定存在重复数字。下面是一个二分法的模板，可以

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int findDuplicate(vector<int> &nums) {
        int len = nums.size();     
        int left = 0;
        int right = len - 1; 

        while (left < right) {
            int mid = (left + right + 1) >> 1;    //n/2
            int counter = 0;
            for (int num:nums) {
                if (num < mid) {  
                    counter++;    
                }
            }

            if (counter >= mid) {   
                right = mid - 1;
            } else {
                left = mid;
            }
        }
        return left;
    }
};

二、LeetCode 35

三、最大值最小化问题

考虑下列问题，把一个包含$n$个正整数的序列划分为$m$个连续子序列，设第$i$个序列各数之和为$S(i)$，你的任务是让所有$S(i)$的最大值尽量小，例如序列1 2 3 2 5 4，划分为3个序列的最优方案为1 2 3| 2 5 | 4，其中$S(1)$、$S(2)$和$S(3)$分别为6、7、4，最大值为7，如果划分为1 2|3 2|5 4，最大值为9，不如刚才的好。

思路

最大值尽量小是一种常见的优化问题，我们考虑一个新问题，能否把输入序列划分为$m$个连续子序列，使所有$S(i)$均不超过$x$？那么让答案为真的最小的$x$就是原题的答案，接下来随便猜一个数字$x_0$，如果不满足，那么说明答案比$x_0$大，否则答案小于等于$x_0$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

#include<cstdio>
#include<cstring>
#define MAXN 505
using namespace std;
int m, k;
long long arr[MAXN], sum, min, ans;
bool vis[MAXN];
 
 
inline int divide(long long M){   //对数组进行划分，返回的是当最大值为M时，所需的划分组数的最小值，即最少需要分为多少组，才能满足最大值最小化的要求
    memset(vis, 0, sizeof(vis));
    int cnt=0;
    int pos=m-1;
    while(pos>=0){
        long long sum=0;
        bool ok=true;
        while(pos>=0 && sum+arr[pos]<=M){    //如果该组目前还小于最大值，说明还可以继续往里添加数
            ok=false;
            sum += arr[pos];
            --pos;
        }
        if(ok){
            return k+1; // 返回一个大于k的数，说明划分的组数超过了k，M不满足要求
        }
        if(pos>=0) vis[pos] = true;  
        ++cnt;  
    }
    return cnt;  //返回划分的组数
}
 
long long binary(){
    long long left=min, right=sum, mid;
    while(left<right){
        mid = (left+right)>>1;
        if(divide(mid)<=k)     //说明所需的组数小于k，则还可以添加新组，最大值可以继续缩小
            right=mid;
        else              //所需组数大于k，说明不能再添加新组，最大值应当适当扩大
            left=mid+1;
    }
    return right;
}
 
inline void output(){
    int cnt=divide(ans);
    for(int i=0; i<m-1&&cnt<k; ++i)if(!vis[i]){  //返回的组数有可能小于k，那么说明还有几组空闲，那么我在任意多划分几组，满足要求即可
        vis[i]=true;
        ++cnt;
    } 
    for(int i=0; i<m; ++i){
        if(i) printf(" %lld",arr[i]);
        else printf("%lld",arr[i]);
        if(vis[i]){
            printf(" /");
        }
    }
    puts("");
}
 
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&m,&k);
        sum=0;  min=0;
        for(int i=0; i<m; ++i){
            scanf("%lld",&arr[i]);
            sum += arr[i];
            if(arr[i]>min) min=arr[i];
        }
        ans=binary();
        output();
    }
    return 0;
}
————————————————
版权声明：本文为CSDN博主「shuangde800」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/shuangde800/java/article/details/7828695

常见搜索算法应用场景

BFS及DFS应用

迷宫类题目

深度及广度优先搜索有一个重要的应用就是在迷宫中寻找路径。本节将针对该类问题进行一个总结。

  1. 处理迷宫方向

我们可以使用方向向量，处理迷宫中任务的移动方向，方向数组如下：

1
2
int dx[2] = {0, 1, -1,  0};   //下、右、左、上
int dy[2] = {1, 0,  0, -1};

  1. 参考文献

0%