数组

本文将针对数组的相关知识进行总结。

数组基本性质

• 一个长度为$N$的数组共有$\frac{(1+N)N}{2}$个子数组

特殊数组

树状数组（Binary Indexed Tree）

数组基本操作

从非起始位置遍历

有些时候，我们需要从数组的中间某个位置开始，对数组进行遍历。我们可以写两个循环，第一个循环遍历后半部分，第二个循环从0开始遍历前半部分，但是更简洁的写法如下：

for(int i = 0; i < length; ++i){
    array[(pos + i) % length] = 0;   // pos是数组中间某个位置
}

求两个数组交集

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        set<int> nums1_set(nums1.begin(),nums1.end());
        set<int> res_set;

        for(int i =0; i < nums2.size();++i)
            if(nums1_set.find(nums2[i]) != nums1_set.end())  //set寻找语句
                res_set.insert(nums2[i]);      //set插入语句

        return  vector<int>(res_set.begin(),res_set.end());
    }
};   //这段代码能够找到两个数组中相同的元素，但是如果两个数组中存在重复元素，并不能找到

LeetCode 面试题 16.15. 珠玑妙算

class Solution {
public:
    vector<int> masterMind(string solution, string guess) {
        vector<int> ans(2,0);
        unordered_map<char,int> s,g;//双字典记录
        for(char c: solution){
            if(s.find(c)==s.end()) s[c]=1;
            else s[c]++;
        }
        for(char c: guess){
            if(g.find(c)==g.end()) g[c]=1;
            else g[c]++;
        }        
        //这里采用双字典，即使有重复元素，也能够找到
        for(unordered_map<char,int>::iterator it=s.begin();it!=s.end();it++){//计算“猜中“和“伪猜中”的总个数
            if(g.find((*it).first)!=g.end()) 
                ans[1]+=min((*it).second,g[(*it).first]);
        }
        for(int i=0;i<4;i++){
            if(solution[i]==guess[i]){
                ans[0]++;//“猜中“
                ans[1]--;//总个数-“猜中“=“伪猜中”
            }
        }
        return ans;
    }
};

string转整数

int ans = 0;
int(i=0;i<nums.size();i++){
    ans = ans*10+nums[i];   //十进制就乘10，二进制就乘2
}

LeetCode1018 可被 5 整除的二进制前缀

数组特殊操作

寻找数组中特定元素类

寻找多数元素

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

思路

这里介绍一种莫尔投票法，初始选择一个数作为众数候选人，然后遍历，如果下一个元素等于众数，那么票数+1，否则票数-1，如果票数为-1，那么说明需要更换候选人，代码如下：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int candidate = -1;
        int count = 0;
        for (int num : nums) {
            if (num == candidate)
                ++count;
            else if (--count < 0) {
                candidate = num;
                count = 1;
            }
        }
        return candidate;
    }
};

找到前三大的数和前2小的两个数

for (int n: nums) {
    if (n <= min1) {
        min2 = min1;
        min1 = n;
    } else if (n <= min2) {     // n lies between min1 and min2
        min2 = n;
    }
    if (n >= max1) {            // n is greater than max1, max2 and max3
        max3 = max2;            
        max2 = max1;
        max1 = n;
    } else if (n >= max2) {     // n lies betweeen max1 and max2
        max3 = max2;
        max2 = n;
    } else if (n >= max3) {     // n lies betwen max2 and max3
        max3 = n;
    }
}

前缀和

字符串

字符串常见性质

1. 一个长度为$n$的字符串的字串一共有$n!$个

字符串常见操作

字符串分割¹

C++

std::string data = "1_2_3_4_5_6";
std::stringstream ss(data);
std::string item;
cout << data << endl;
while (std::getline(ss, item, '_'))    //以指定字符_对字符串进行分割
    cout << item << ' ';

//使用正则表达式匹配
regex ws_re("\\s+");
vector<string> v(sregex_token_iterator(s.begin(),s.end(),ws_re,-1), sregex_token_iterator());
for(auto &n:v){
    cout << n << endl;
}

//手工实现字符串分割，其中s表示被分割的字符串，c表示分割符
void SplitString(string & s,string & c, vector<string>& v) {
    std::string::size_type pos1 = 0, pos2 = s.find(c);
    while (string::npos != pos2){
        v.push_back(s.substr(pos1, pos2 - pos1));
        pos1 = pos2 + c.size();
        pos2 = s.find(c, pos1);
    }
    if (pos1 != s.length())
        v.push_back(s.substr(pos1));
}

//记录字符串中单词的个数（此处单词为广义单词，仅为字符串被空格分隔的片段个数）
//这里采用了一种倒序法，判断字母前一个位置是否为空格，如果是，说明此处出现新单词，当然第一个单词需要额外进行判断
int countSegments(string s) {
    int ans = 0;
    for(int i=0;i<s.size();i++){
        if( (i == 0 || s[i-1] == ' ' ) && s[i] != ' ') ans++;
    }
    return ans;
}

上面的方法有一些问题，如果字符串中包含有多个连续空格，那么会产生空的子字符串，所以需要进行特判，将这些空子字符串进行排除。

字符串提取字串

KMP算法

KMP算法能够在$O(m+n)$的时间复杂度实现两个字符串的匹配。所谓匹配，指给定字符串S和模式串P，判断P是否为S的子串。

C语言

char *buff = "this is a test string";
char subbuff[5];
memcpy( subbuff, &buff[10], 4 );   //提取从buff[10]开始的4个长度的字符串
subbuff[4] = '\0';

string用法总结

string本质上是一个特化的容器类，可以视为vector<char>。本节对string的常用方法进行总结。

拷贝构造

string ans(s.begin()+n,s.end());     //注意拷贝范围是0至end-1,左闭右开区间

提取子string

string a = s.substr(0,5);     //获得字符串s中从第0位开始的长度为5的字符串

实现strstr函数

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

int strStr(string& haystack, string& needle) {

    int first = 0, second = 0;
    while(first < haystack.size() && second < needle.size()){
        if(haystack[first] != needle[second]){
            first = first-second+1; //回溯，从下一个位置开始搜索
            second = 0;             //回溯，将指针回至0
        }
        else{
            first++;
            second++;
        }
    }
    if(second >= needle.size()) return first - needle.size();
    else return -1;
}

使用计数器处理string中字符

在有些情况下，我们需要统计string中出现字符的次数，如果仅仅考虑26个英文单词，那么我们可以设置一个大小为26的vector，然后将对应位加一，例如LeetCode242. 有效的字母异位词

判断两个string是否包含相同的字母，只是字母顺序发生变化，那么我们可以设置一个计数器，遍历两个string，一个对计数器递增，一个递减，最后判断是否都为0即可。

LeetCode 49. 字母异位词分组

字符串原地替换

在有些时候，我们需要将字符串中某些字符进行替换，例如在字符串URL化过程中，我们需要将空格替换为‘%20’，这种情况下我们需要进行两步操作

• 对字符串进行空间扩充
• 利用双指针，一个指向最后一个不为空格的字符，另一个指向字符串的末尾，从后往前进行替换，这样可以保证不会把前面的替换掉

字符串相同字符统计

给定下面的代码，可以统计字符串中包含相同字符的子串的个数：

int countLetters(char * S){
    int n = strlen(S);
    int ans = 0;
    int count = 1;
    for (int i = 1; i < n; i++) {
        if (S[i-1] == S[i])
            count++;
        else {
            ans += (count * (count + 1) / 2);
            count = 1;
        }
    }
    ans += (count * (count + 1) / 2);
    return ans;
}

高维数组

高维数组索引

LeetCode面试题04 二维数组中的查找

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]

这类数组有一个特点，即存在标志数，即左下角或右上角元素，左下角元素为所在列最大元素，所在行最小元素。将该标志数记为flag，则有

• flag > target：说明target一定在flag之上，即flag所在行可以消去，即(row—)
• flag == target：找到返回
• flag < target：说明target在flag右侧，flag所在列可以消去(col++)

专题：区间问题

高维子数组

当我们处理迷宫问题或者进行图像处理时，往往需要分析高维数组的子数组，此时我们可以借助方向矩阵或者子数组提取循环，这样可以避免写出大量的边界判断语句

//获取3×3的子矩阵
for (int nr = r-1; nr <= r+1; ++nr)
    for (int nc = c-1; nc <= c+1; ++nc) {
        if (0 <= nr && nr < R && 0 <= nc && nc < C)

LeetCode上关于数组的题目

专题：大数相加问题

class Solution {
public:
    string addStrings(string num1, string num2) {
        stack<char> ans_stack{};
        string ans{};
        int flag{0};
        int curr_ans{0};
        while(!num1.empty() && !num2.empty()){
            curr_ans = (num1[num1.size()-1] - '0') + (num2[num2.size()-1] - '0') + flag;
            flag = curr_ans / 10;
            curr_ans %= 10;
            ans_stack.push(curr_ans+'0');
            num1.erase(num1.size()-1);
            num2.erase(num2.size()-1);
        }
        while(!num1.empty()){
            curr_ans = (num1[num1.size()-1] - '0') + flag;
            flag = curr_ans / 10;
            curr_ans %= 10;
            ans_stack.push(curr_ans+'0');
            num1.erase(num1.size()-1);
        }
        while(!num2.empty()){
            curr_ans = (num2[num2.size()-1] - '0') + flag;
            flag = curr_ans / 10;
            curr_ans %= 10;
            ans_stack.push(curr_ans+'0');
            num2.erase(num2.size()-1);
        }
        if(flag!=0){
            ans_stack.push(flag+'0');
        }
        while(!ans_stack.empty()){
            ans += ans_stack.top();
            ans_stack.pop();
        }
        
        return ans;
    }
};

思路并不复杂，但是这个模板比较常用，建议熟练掌握，其中使用栈对结果进行了保存。

专题：子序列问题

42 接雨水²

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

思路1 按列求+动态规划

一列一列求雨水，然后按照木桶原理，确定左右两端最高的墙。

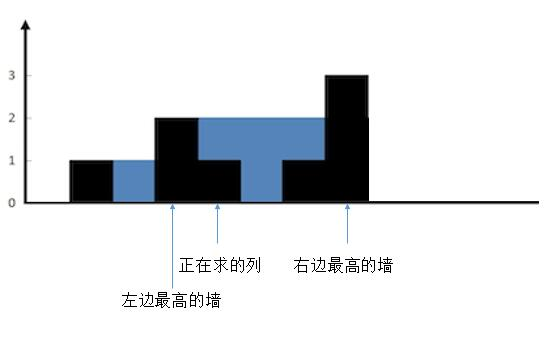
只有当正在求的列高度小于min(max_left,max_right)，才能够存储水，为了找到每个列两侧最大值，普通方法是遍历，会重复求解，可以利用动态规划，设置两个数组，max_left [i]代表第 i 列左边最高的墙的高度，max_right[i] 代表第 i 列右边最高的墙的高度。

对于 max_left我们其实可以这样求:max_left [i] = Max(max_left [i-1],height[i-1])

代码如下：

class Solution {
public:
    int trap(vector<int>& height) {
        if(height.empty()) return 0;
        int ans{0};
        
        int *max_left = new int[height.size()]{0};
        int *max_right = new int[height.size()]{0};
        
        for(int i=1;i <= height.size()-1;i++){
            max_left[i] = max(max_left[i-1],height[i-1]);
        }
        
        for(int i=height.size() - 2;i>=0;i--){
            max_right[i] = max(max_right[i+1],height[i+1]);
        }
        
        for(int i=1;i<height.size()-1;i++){
            
            int min_wall_height = min(max_left[i],max_right[i]);
            if(min_wall_height > height[i]){
                ans += min_wall_height - height[i];
            }
        }
        return ans;
    }
};

参考文献

---

1. 1.字符串分割 ↩
2. 2.接雨水参考答案 ↩