你站在桥上看风景,看风景的人在楼上看你。明月装饰了你的窗子,你装饰了别人的梦。——《断章》
递归简介
递归组成
递归由两部分组成:
- 锚或者叫基例,顾名思义,它是产生集合中其他元素的基本元素(基例是递归调用链中最后一步,用于停止递归,可以避免陷入无限循环)
- 构造规则,用于由基本元素或已有对象产生新对象的构造规则
递归的例子
二叉搜索树,比当前结果小,搜索左树,否则搜索右树。
递归优缺点
优点:
- 使程序简洁易读,当我们能够确定,大问题能划分为相似的小问题时,我们可以用递归
- 递归在栈、树及图中广泛应用(我们可以使用循环,但较复杂)
- 递归在排序、分治、贪心和动态规划中广泛使用
- 递归一般是自底向上进行搜索,例如二叉树的前序遍历,递归过程是一路搜索到最下端,然后从叶子节点向上逐步返回
缺点:
空间时间效率都不如迭代,递归调用过程会使用栈,所以空间消耗也要考虑进去。
综上,当我们能够将大问题拆分为小问题,不在乎时间空间消耗,想要尽快编写一个解而不考虑效率, 可以使用递归。
递归的实现
注:这一部分涉及递归调用在c++中的实现,如果不需要了解递归过程中函数是如何调用的,可以跳过这一段,一句话来说递归是通过压栈入栈实现的。所以如果有需要栈实现的问题,也完全可以使用递归实现,例如面试题06. 从尾到头打印链表
1 | vector<int> reversePrint(ListNode* head) { |
不同的递归类型
尾递归
尾递归的定义是递归调用是递归函数的最后一条语句,并且在此之前也没有其他直接或间接递归调用,对于前面的状态不需要保存。
1 | void fun(int n){ |
上面的程序输出为3 2 1。
如何理解对于前面的状态不需要保存呢?看上面的代码,我们知道递归调用是一个不断压栈的过程,而由于尾递归中递归是最后一条语句,返回后没有别的语句需要执行,因此直接出栈即可。
| Push | Pop | Pop | Pop | Pop | |
|---|---|---|---|---|---|
| fun(0) | return | ||||
| fun(1) | 执行prinf; Act f1 | Act f1 | |||
| fun(2) | 执行prinf; Act f2 | Act f2 | Act f2 | ||
| fun(3) | 执行prinf; Act f3 | Act f3 | Act f3 | Act f3 | |
| main | Act m | Act m | Act m | Act m | Act m |
非尾递归
与尾递归相对应的是非尾递归,即递归不是函数中的最后一条语句,递归函数返回之后有一些遗留的东西需要处理。
1 | void fun(int n){ |
| Push | Pop | Pop | Pop | Pop | |
|---|---|---|---|---|---|
| fun(0) | return | ||||
| fun(1) | Act f1 | Act f1 | 执行printf(“1 “) | ||
| fun(2) | Act f2 | Act f2 | Act f2 | 执行printf(“2 “) | |
| fun(3) | Act f3 | Act f3 | Act f3 | Act f3 | 执行printf(“3”) |
| main | Act m | Act m | Act m | Act m | Act m |
输出结果为1 2 3,所以非尾递归可以用于倒序输出。
注意:非尾递归转换为迭代形式,需要显式使用栈操作。
一个容易迷惑的例子,看似是尾递归,实则是非尾递归:
1 | int fact(n) { |
因为在函数返回后,需要计算n * fact(n - 1),因此以前的结果需要保留。计算过程分为如下两个部分:
- 将递归函数逐层展开
1 | (5 * fact(4)) |
- 自底向上计算并合并结果
1 | (5 * (4 * (3 * (2 * 1))))) |
所以普通的尾递归其实效率并不高。
常见递归算法
深度优先搜索
本节请参考
回溯
回溯是深度优先搜索的一种,也是一种常用的暴力搜索方法,可以找出一部分或所有解,回溯法在最坏情况下复杂度为指数时间。应用场景在后续结果依赖于前面的选择。
回溯法要点
回溯法本质上是递归的一种,所以在考虑的时候要从递归的特点入手,着重解决递归退出的条件。使用回溯的问题可以被视为一个多叉树,树的深度取决于给定元素的个数。一条从根节点到叶节点的路径即为一个可行解。本节将针对回溯法的要点与难点进行分析,并总结常见的回溯形式。
回溯法基本步骤
- 抽象问题,将问题转换为“排列、子集、组合”的一种
- 画出递归树,找到状态变量(回溯函数的参数)
- 树的总深度(数组的长度,链表的长度)
- 当前深度
- 搜索集合
- 根据题意,确立结束条件
- 找准选择列表(与函数参数相关),与第一步紧密关联※
- 判断是否需要剪枝
- 作出选择,递归调用,进入下一层
- 撤销选择
回溯法基本框架
1 | void back_track(...){ |
第一类,寻找全部解的回溯法
一 树或链表类:此类问题要求寻找树或链表中全部解或者统计解的个数,因此在找到解的时候,不能返回,需要对解进行记录,该类问题的回溯法算法流程如下:
- 输入递推参数:当前节点root,目标值target,解空间ans,临时解temp_ans;
- 判断终止条件:当root == nullptr时,返回
- 进行递推工作
- 临时解更新,将当前root->val加入temp_ans;
- 目标值更新,target = target - root->val;
- 解空间更新,当 target 为 0(满足目标值)并且满足其他特定条件时,将此临时解加入解空间
- 深度优先搜索,更新相关参数
- 路径恢复,将root->val 从 temp_ans中弹出。
例题1 LeetCode面试题34 二叉树中和为某一值的路径
二 一维数组类:此类问题要求寻找数组中全部解或统计解个数,该类问题的回溯法算法流程如下:
- 输入递推参数:递归树深度或数组长度n,解空间ans,临时解temp_ans,当前深度first
- 判断终止条件:当first == n,即搜索已经超过数组长度时
- 进行递推工作
- 临时解更新,
第二类,寻找解是否存在的回溯法
剪枝处理
剪枝一般出现在需要去除重复或者不符合条件的解的场合,参考LeetCode中非重复的全排列。剪枝过程包括如下几个流程:
- 创建visited数组,用于判断当前节点是否已经访问
- 对待处理的数组进行排序处理,从而保证能够通过num[i-1] 是否等于 num[i]确定是否需要剪枝
- 递归时将visited置1,回溯时置0
1 | void backtrack(vector<vector<int>>& ans, vector<int>& nums, vector<int>& curr, vector<int>& visited){ |
回溯法常见应用:
组合
一. 组合,求$C_n^k$,这个模板也很常用
1 | class Solution { |
正确理解上面的代码是很重要的,接下来我们将以图示的形式解释其中的关键部分:
1 | for(int i=first;i<=n;i++){ |
二. 可重复被选取的组合:LeetCode 39
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
1 | 输入: candidates = [2,3,6,7], target = 7, |
这种题目一看就是用回溯法,但是本题有一个条件,就是数字可以无限制重复被选取,这意味着我们在回溯的循环过程中,每一次回溯start都是i。另外求总和等于target,可以采用自顶向下的方法,即每次减去一个数
1 | for (int i = start; |
在调用深度优先搜素时,必须先对nums进行排序,才能进行减枝处理。
排列
一. 非减枝全排列
给定一个没有重复数字的序列,返回其所有可能的全排列。
1 | 输入: [1,2,3] |
思路:我们在写全排列问题时,一般是先确定一位,然后对剩下的子数组进行全排列,才能做到不重复也不遗漏,传统循环方式肯定是行不通的,时间复杂度过高。回溯法将问题转换为对树的搜索问题,通过深度优先遍历 + 状态重置(回溯) + 剪枝(可选),实现全排列的搜索。
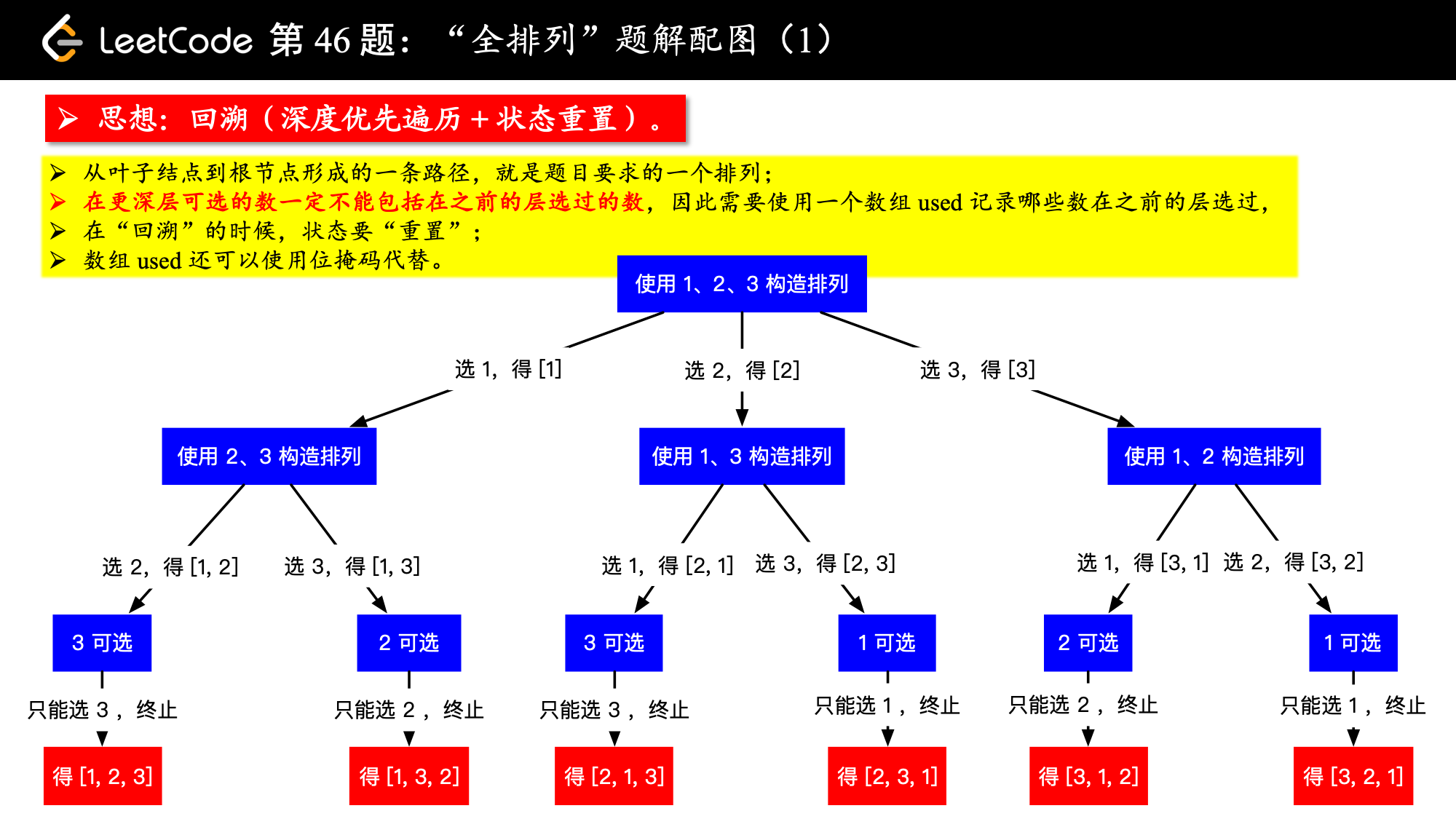
在每一层,我们都有若干条分支供我们选择。下一层的分支数比上一层少 1 ,因为每一层都会排定 1 个数,从这个角度,再来理解一下为什么要使用额外空间记录那些元素使用过;全部的“排列”正是在这棵递归树的所有叶子结点。
代码如下:
1 | class Solution { |
二. 剪枝全排列
如果需要排除重复的情况,那么就是带有减枝的操作,如leetcode47及1079,非重复的全排列,题目如下:
给定一个可包含重复数字的序列,返回所有不重复的全排列。
1 | 输入: [1,1,2] |
这个模板很通用,记住(这个代码还需要多理解几次)
1 | class Solution { |
这里比较让人迷惑的是减枝条件判断的第三个条件,其解释如下:
以 [2, 3, 3, 3] 中的 3 个 3 为例,相同的 3 个 3 有 6 个排列。我们只要保留 1 个就好了。
它们的索引分列是:
[1, 2, 3] (数组中的数组表示 3 这个元素在 [2, 3, 3, 3] 这个数组中的索引,在全排列中可能的“排列”,下同)
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
发现其实又是一个全排列问题。首先联系数组 used[i - 1] 的语义:used[i - 1] == true 表示索引 i 位置的前一个位置元素已经使用过。在 used[i - 1] == true 的时候全部 continue 掉,则只剩下了 used[i - 1] == false 的情况,即当前遍历的元素的之前的元素均未使用过,因此保留了 [3, 2, 1] 这种排列。作者:liweiwei1419
链接:https://leetcode-cn.com/problems/permutations-ii/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liwe-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
三. 下一个排列
四. 第K个排列
给出集合[1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
1 | "123" |
给定 n 和 k,返回第 k 个排列。
思路
排列的每种情况均可以使用十进制或者二进制的形式进行表示,相当于使用掩码对排列进行操作:
五. N皇后问题
1 | class ChessBoard{ |
子集
子集(leetcode 78)
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
1 | 输入: nums = [1,2,3] |
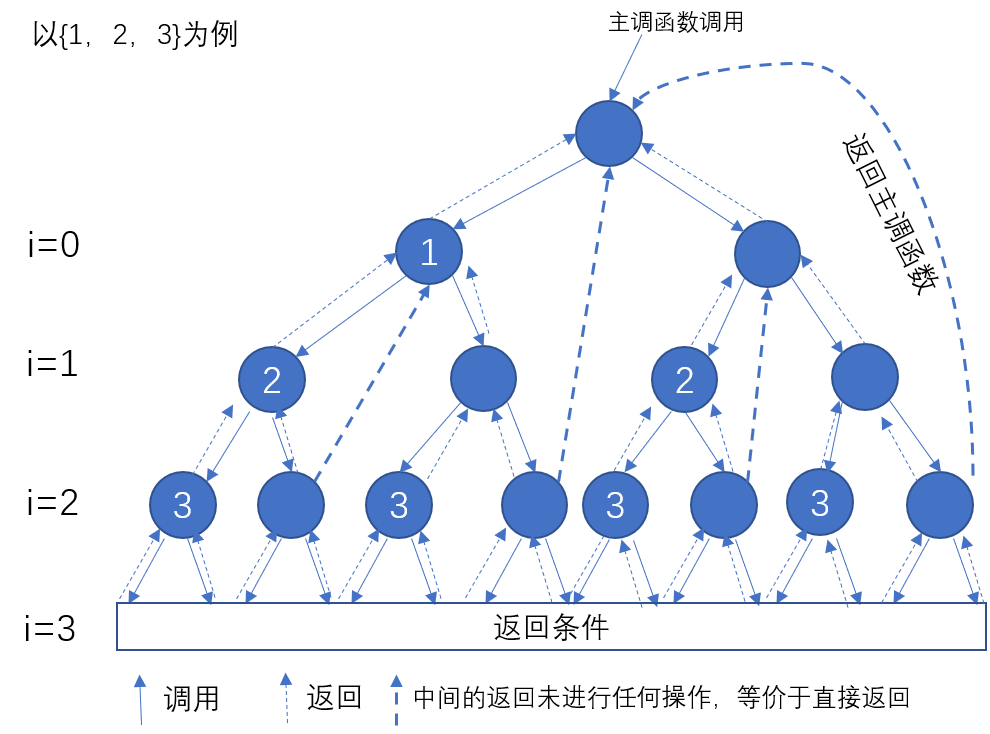
递归问题最重要的就是找到基例和构造规则,本题基例不难找,关键是构造规则比较麻烦
1 | void compute(vector<vector<int>>&subset_set, |
这种题的一般思路就是一个元素一个元素往上加,先考虑集合中只有一个元素的情况,然后一个元素讨论清楚了,再考虑两个元素,一般两个元素就能找到回溯规律。本题可以等价为二叉树遍历的问题,子集中选不选择某个元素,就可以视作是yes or no问题,是一个典型的二分类。
分治法
在计算机科学中,分治法是构建基于多项分支递归的一种很重要的算法范式。字面上的解释是「分而治之」,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序、归并排序)、傅立叶变换(快速傅立叶变换)。分治法的思路如下所示:
graph TB
node["原问题"]
node1["子问题"]
node2["子问题"]
node3["子问题的解"]
node4["子问题的解"]
node5["原问题的解"]
node-->node1
node-->node2
node1-->node3
node2-->node4
node3-->node5
node4-->node5
分治法应用场景
分治法最适用于能够将大问题拆分成两个或多个相似子问题的场景。
递归使用步骤
递归使用过程中常见步骤如下:
- 确定返回值的意义
- 确定返回值是否需要保存
- 确定基例
- 确定递归构造规则
递归难点总结
使用递归时,尽可能保证递归体的简单性
由于递归可能涉及复杂的出入栈操作,因此在一定程度上会导致程序分析困难,所以应当尽可能保证递归体简洁性,保证一个递归操作只完成一个任务。例如LeetCode 面试题36:
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
思路比较简单,先创建一个vector,中序遍历保存所有节点,然后将节点依次相连即可。在编写代码过程中,我们将中序遍历单独写为一个递归函数,实现节点遍历及保存的功能。相关代码如下:
1 | /* |
递归与分治
递归实际上包含了分治的思想,将大问题逐步拆解成简单的小问题,因此我们在使用递归时,一个非常重要的步骤就是找到分治的方法。我们将以 汉诺塔问题对找到分治的过程进行总结。
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
考虑一个盘子,那么我们直接将盘子从A移动至C,即C.push_back(A.pop_back());
当有两个盘子时,我们首先将小盘子移动至B,然后将大盘子移动至C,最后将小盘子移动至C,这个过程为:
1 | B.push_back(A.pop_back()); |
当有n个盘子时,我们可以将盘子分成两部分,n-1个小盘子先移动到B,然后将最后一个大盘子移动到C,最后将n-1个小盘子移动到C,这个过程可以写为:
1 | move(n-1, A, C, B); //n-1个小盘子移动到B |
完整代码如下:
1 | void hanota(vector<int>& A, vector<int>& B, vector<int>& C) { |