链表 | 一隅

本文将对链表相关知识进行一个总结。

什么是链表

链表是一种长度可变的线性数据结构（线性的意思是列表中每个节点只能访问相邻节点，不能跨节点访问），链表中每个节点都是一个独立元素（不影响其他节点），一个节点由三部分组成：

value
指向下一个节点的指针
节点自身的地址

链表图示

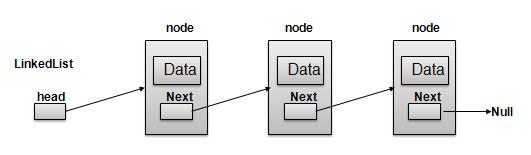
链表的组成

链表由如下部分组成：

Node：包括值和指向下一个节点的指针
Head：指向第一个节点的指针，用于访问链表第一个Node
Tail：指向最后一个节点的指针，用于访问最后一个Node，从而方便添加尾节点（否则需从头遍历，效率很低）

链表类型及作用

链表类型

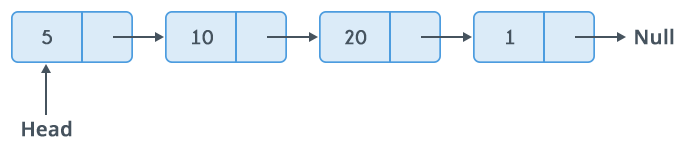
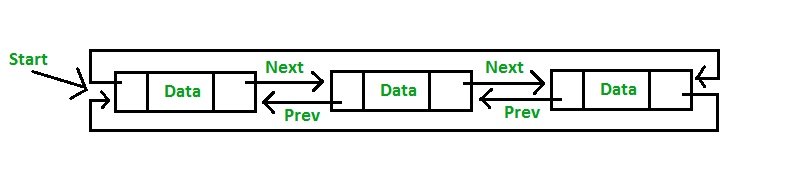
单向链表，Single Link List（SLL）：保存后向节点的指针，不保存前向的（一条蛇）
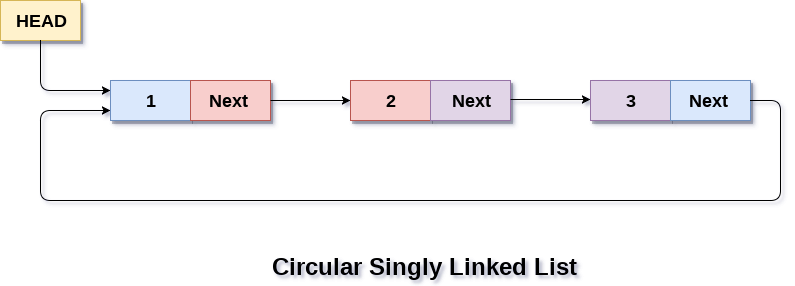
循环单向链表，Circular SLL：与SLL唯一的区别是最后一个节点保存第一个节点的指针（一条咬住尾巴的蛇）
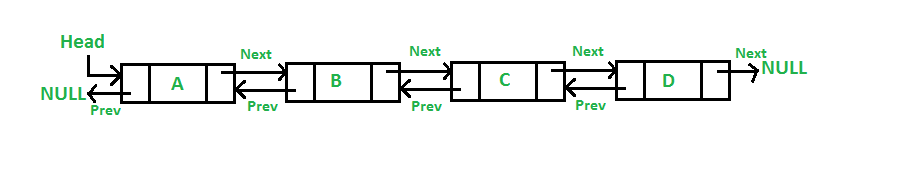
双向链表，DLL：保存前向和后向节点的指针，一个节点可访问前向和后向（一列火车）
循环双向链表，CDLL（一列首尾相连的火车）
作用

SLL是最基本的链表类型，用于运行期添加删除元素。

CSLL为了解决SLL不能循环访问的缺点，想象一个下棋游戏，最后一个玩家进行完后需要返回，由第一个玩家进行，SLL不能胜任这种任务，但是CSLL可以。

DLL为了解决SLL不能前向访问的缺点，想象一个音乐播放器，当我们按下上一首，下一首，我们希望访问前一个和后一个节点，这种情况下使用双向链表可以解决这种问题。

CDLL则兼具CSLL和DLL的优点，可以循环及前向访问。

链表基本操作

链表基本操作包括：

链表的创建与删除
链表插入
链表遍历
链表搜索
链表节点删除

单向链表的操作

单向链表的建立

创建Head和Tail并初始化为Null
建立节点1·，节点1指向Null
将Head与Tail指向节点1

时间与空间复杂度都是$O(1)$。

单向链表的插入

插入分为三种：在头在尾在中间。三种操作都需要创建一个新节点。

在头插入

将新节点指向第一个节点（即Head中的值）
将Head指向新节点

在尾插入

将最后一个节点指向新节点
将Tail指向新节点

在中间插入

将新节点指向被插入点后的节点
将被插入点前的节点指向新节点

insert(head, node_value, location){
    create a new node
    node.value = node_value;
    if(head = null)
        return error // SLL does not exist
    
    else if(location == 0)  //在头插入
        node.next = head
        head = node
    else if(location == last)  //在尾部插入
        node.next = null
        tail.next = node
        tail = node
    else  //在中间插入
        loop:tmp_node = 0 to location - 1  //tmp_node 就是被插入的节点
        node.next = tmp_node.next
        tmp_node.next = node
}

时间复杂度为$O(n)$，空间复杂度为O(1)。

链表的遍历与搜索

时间复杂度$O(n)$，空间为$O(1)$。

链表节点的删除

删除头节点

如果只有一个节点，那么使用一个临时Node指针保存头节点，然后将Head和Tail指向nullptr，最后删除tmp。

如果有多个节点，将Head指向Head->next。

删除尾节点

如果只有一个节点，那么使用临时节点保存尾节点，然后Head和Tail置空，最后删除tmp。

如果有多个节点，需要进行遍历，找到倒数第二个节点，将其next置空并另Tail指向它。然后删除tmp

删除中间节点

遍历找到待删除的前一个节点，临时Node指针保存待删除节点，将前一个节点指向待删除节点next，然后删除待删除节点。

获取中间节点

可以采用快慢指针的方式获取中间节点，如果需要从中间节点之前断开链表，可以使用另外一个额外的变量prevPtr对中间节点之前的节点进行保存

ListNode* findMid(ListNode* head){
    ListNode* slow, *fast, *prev;
    prev = nullptr;
    slow = fast = head;
    while(fast != nullptr && fast->next != nullptr){
        prev = slow;             //保存中间节点的前一个节点
        slow = slow->next;
        fast = fast->next->next;
    }
    if(prev != nullptr){
        prev->next = nullptr;   //从中间节点前断开，中间节点属于后半部分
    }
    return slow;
}

双向链表的操作

链表高级操作

merge(l1,l2)，双路归并
cut(l,n)，断链操作，将链表l切掉前n个节点，并返回后半部分链表头
reverse，反转操作
删除特定节点

merge操作

将两个List排序后合并，过程和数组的合并比较类似，就是链表操作过程比较麻烦。

迭代法

ListNode* merge(ListNode* l1, ListNode* l2) {
    ListNode dummyHead(0);   
    auto p = &dummyHead;   //p是辅助指针
    while (l1 && l2) {     
        if (l1->val < l2->val) {
            p->next = l1;             
            p = l1;                  
            l1 = l1->next;           
        } else {
            p->next = l2;               //
            p = l2;                     //移动p
            l2 = l2->next;              //移动l2，相当于数组中的i++操作
        }
    }
    p->next = l1 ? l1 : l2;             //将剩余部分合并到链表中
    return dummyHead.next;
}

递归法

递归法的递推公式如下，先选出两个节点中较小的那个，然后将剩下的部分递推，返回值是较小链表节点的指针。

$\left\{\begin{array}{ll} \operatorname{list} 1[0]+\operatorname{merge}(\operatorname{list} 1[1:], \text {list2}) & \operatorname{list} 1[0]<\operatorname{list} 2[0] \\ \operatorname{list} 2[0]+\operatorname{merge}(\operatorname{list} 1, \operatorname{list} 2[1:]) & \text {otherwise} \end{array}\right.$

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    if(l1 == nullptr) return l2;
    else if(l2 == nullptr) return l1;
    else if(l1->val <= l2->val){
        l1->next = mergeTwoLists(l1->next,l2);
        return l1;          //返回较小的链表的节点
    }
    else{
        l2->next = mergeTwoLists(l1,l2->next);
        return l2;
    }
}

cut操作

ListNode* cut(ListNode* head, int n) {
    auto p = head;
    while (--n && p) {
    p = p->next;    //移动头结点
    }

    if (!p) return nullptr;  

    auto next = p->next;    //保存下一节点指针
    p->next = nullptr;      //断开链表
    return next;            //返回下一段链表头节点
}

reverse操作

这是一道很经典的题目，将一个链表进行翻转，可以使用递归和迭代的方式进行操作。

1 2	输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL

迭代法

ListNode* reverseList(ListNode* head) {
    ListNode* prev = nullptr;   //前一个节点
    ListNode* curr = head;      //当前节点

    while(curr!=nullptr){
        ListNode* nextTemp = curr->next;   //后一个节点
        curr->next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

链表里一个比较麻烦的问题就是断链后后一个节点如果不保存，就再也找不到了，因此需要将前一个节点，当前节点和后一个节点都保存起来。链表翻转一定是从头开始的，因为一旦从尾部开始，前面节点的指针就找不到了。

递归法

假设链表为：

$n_1→...→n_{k−1}→n_k→n_{k+1}→...→n_m→\emptyset$

若从节点 $n{k+1} $到 $n{m}$ 已经被反转，而我们正处于 $n_{k}$。

$n_1→...→n_{k−1}→n_k→n_{k+1}←...←n_m$

我们希望$n_{k+1}$指向$n_k$，所以nk->next->next = nk

public ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) return head;
    ListNode p = reverseList(head.next);
    head.next.next = head;   //关键操作
    head.next = null;
    return p;
}

要小心的是 $n_{1}$ 的下一个必须指向 Ø ，否则可能会产生循环。递归的方式还挺麻烦的，最好用栈模型对上面的代码进行一下分析。

删除特定节点

ListNode* removeElements(ListNode* head, int val) {
    if(head == nullptr) return head;
    ListNode* dummy = new ListNode{0};
    dummy->next = head;
    auto p = dummy;
    while(p->next != nullptr){ 
        if(p->next->val == val){   //删除所有node->val == val的节点
            p->next = p->next->next;
        }
        else{
            p = p->next;
        }
    }
    return dummy->next;
}

LeetCode 86

深拷贝

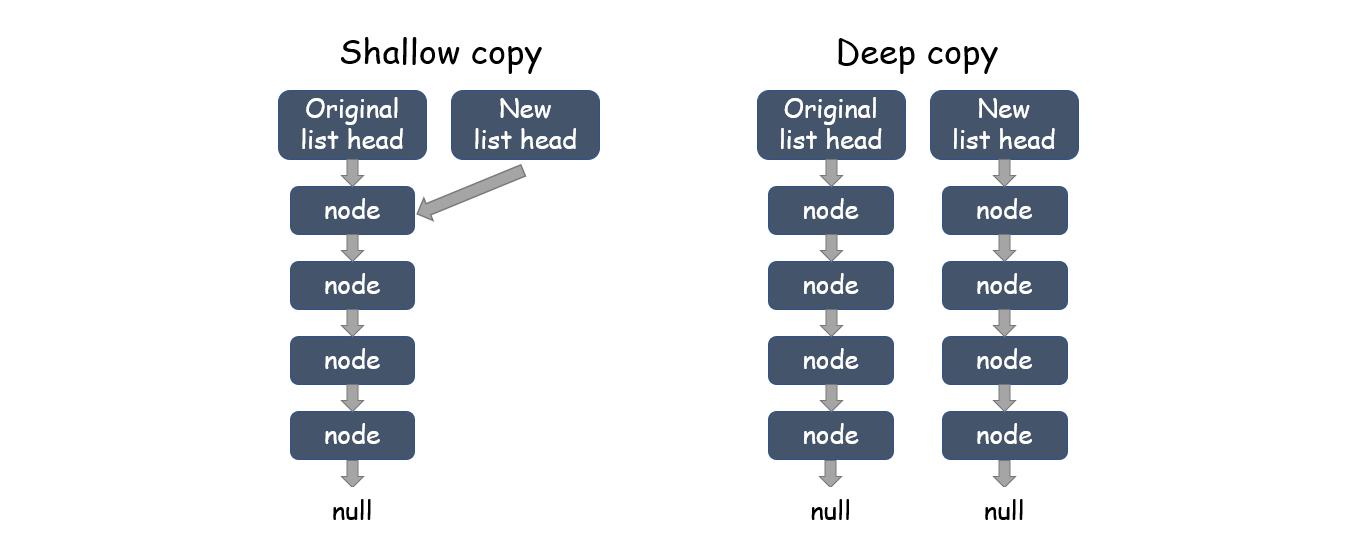
与浅拷贝对应的是深拷贝，浅拷贝只复制指向某个对象的指针，并不复制对象本身，新旧对象共享一块内存。而深拷贝会另外开辟空间，创建新的对象，新旧对象不共享内存，修改新对象不会影响旧对象。

图片名称

练习

LeetCode面试35 复杂链表的复制

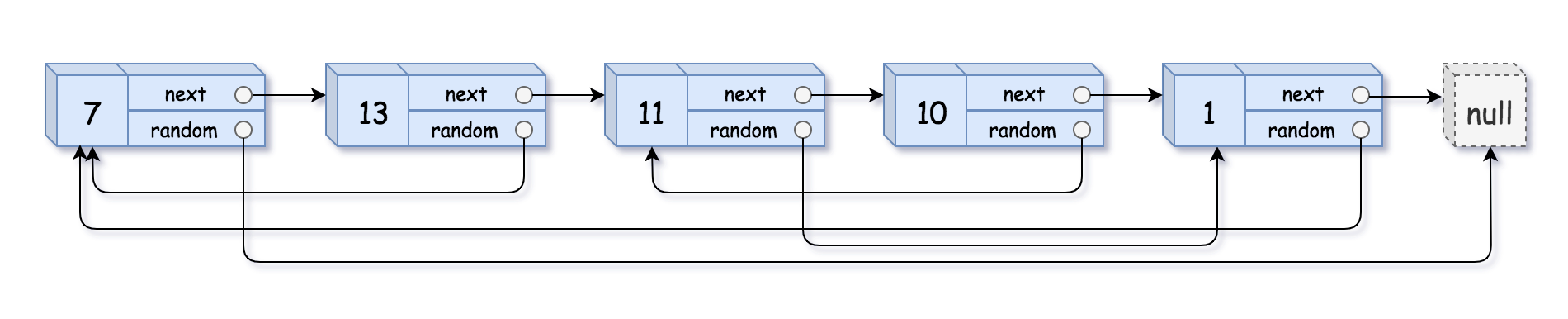
请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

图片名称

思路

链表的复制可以采用DFS方法，关于DFS方法的讨论请参考

代码

Node* copyRandomList(Node* head) {
    if(head == nullptr) return head;
    else if( visited[head] != nullptr) return visited[head];  // 如果已经访问了，说明该节点已经复制，那么直接返回即可

    Node* copy = new Node(head->val);              
    visited[head] = copy;              
    copy -> next = copyRandomList(head->next);
    copy -> random = copyRandomList(head->random);
    return copy;
}

判断是否有环

bool IsExistLoop(Node* head)
{
    Node *slow = head, *fast = head;
    while ( fast && fast->next )
    {
        slow = slow->next;
        fast = fast->next->next;
        if ( slow == fast )
            break;
    }
    return !(fast == NULL || fast->next == NULL);
}

链表难点总结

递归时的返回条件判断

当链表需要进行和两个节点有关的操作时，判断条件为if(head == nullptr || head->next == nullptr)，否则只对链表本身进行判断。迭代也是同样的道理：while(temp.next != null && temp.next.next != null)

LeetCode上关于链表的相关题目

使用链表进行大数相加

给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

1
2
3

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        //设置变量
        ListNode result(0), *p = &result;
        int flag = 0;
        while(l1 || l2 || flag){ 
            //难点1：循环条件
            //当l1不为空或者l2不为空或者需要进位时，都需要创建新节点
            /*************************计算当前两位相加和*************************/
            int tmp_value = 0;
            if(l1 != nullptr) tmp_value += l1->val;  
            if(l2 != nullptr) tmp_value += l2->val;
            tmp_value += flag;   
            
            flag = tmp_value / 10;
            tmp_value %= 10;
            
            /*************************创建新节点，用于保存新值*************************/
            ListNode *next = new ListNode(tmp_value);
            next->val = tmp_value;
            
            /*************************更新节点*************************/
            //难点2： 对于节点更新的处理
            p -> next = next;
            p = p -> next;
            l1 = (l1 != nullptr ? l1 -> next : nullptr);
            l2 = (l2 != nullptr ? l2 -> next : nullptr);
        }
        
        //返回结果
        //难点3： 返回值的处理
        return result.next; //注意返回的结果链表是从result的next开始的
    }
};

Given a linked list, remove the n-th node from the end of list and return its head.

Example:

1
2
3

Given linked list: 1->2->3->4->5, and n = 2.

After removing the second node from the end, the linked list becomes 1->2->3->5.

问题本身不难，两遍法第一遍遍历找到列表长度，第二遍移除$L-n+1$个节点即可，注意，算法题解决过程中下标从1开始，不要从0，否则计算起来很麻烦。

而一个更紧凑的方法是如下代码

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *d = new ListNode(0);
        d->next = head;
        ListNode* first;
        ListNode* second;
        first = second = d;

        for(int i=0;i<=n;i++){
            first = first->next;
            
            if(first == nullptr){
                return d->next;
            }
        }
        while(first != nullptr){
            first = first->next;
            second = second->next;
        }
        second->next = second->next->next;
        return d->next;
    }
};

该代码创建了一个辅助哑节点，哑节点可以简化链表需要删除头节点的情况，注意最后返回的是d->next，不能返回head，因为head有可能已经被删掉了。

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:
1
2
3
4
5
6
7
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6

一般像这种题都有一个暴力解法，本题暴力解法是将所有元素放到一个vector中，然后排序，然后生成新的链表，时间复杂度$O(NlogN)$，N是节点总数目。空间复杂度$O(n)$。

链表的自底向上归并排序

ListNode* sortList(ListNode* head) {
    ListNode dummyHead(0);
    dummyHead.next = head;
    auto p = head;
    int length = 0;
    //计算长度
    while (p) {
        ++length;
        p = p->next;
    }

    for (int size = 1; size < length; size <<= 1) {   //左移相当于乘2
        auto cur = dummyHead.next;   
        auto tail = &dummyHead;    

        while (cur) {
            auto left = cur; 
            auto right = cut(left, size); // left->@->@ right->@->@->@...
            cur = cut(right, size); // left->@->@ right->@->@  cur->@->...

            tail->next = merge(left, right); //两两归并
            while (tail->next) {   //找到merge后的尾节点
                tail = tail->next;
            }
        }
    }
    return dummyHead.next;
}

链表