求方程数值解

本文将针对求解方程数值解的方法进行总结。

牛顿法

原理

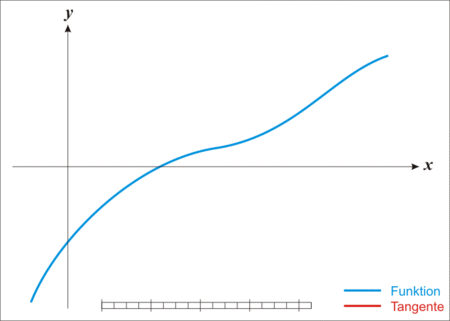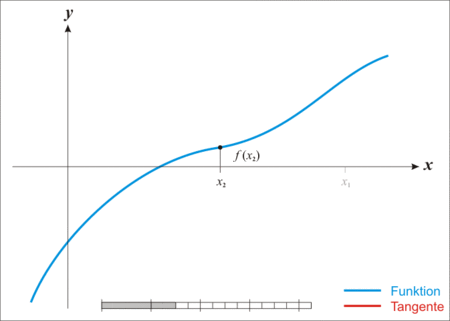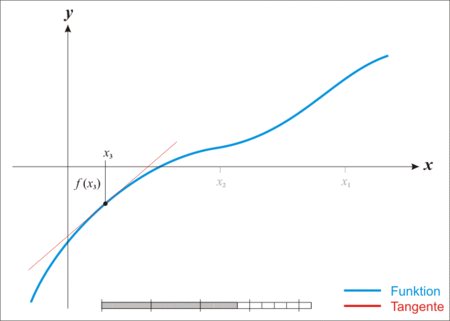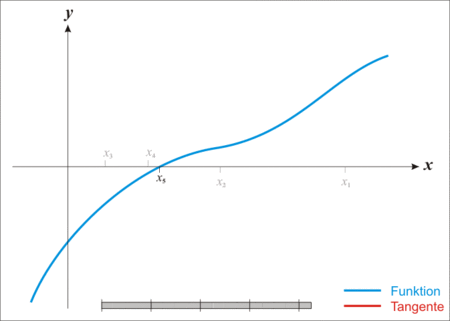
选择一个接近函数$f(x)$零点的$x_0$，计算相应的$f(x_0)$和切线斜率$f’(x_0)$。然后我们计算穿过点$(x_0,f(x_0))$且斜率为$f’(x_0)$的直线和$x$轴交点的$x$坐标，也就是求如下方程解：

$$\begin{equation} 0=\left(x-x_{0}\right) \cdot f^{\prime}\left(x_{0}\right)+f\left(x_{0}\right) \end{equation}$$

然后开始下列迭代公式进行迭代，求解$f(x)=0$的解：

$$\begin{equation} x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)} \end{equation}$$

二次收敛条件

1. $f’(x)\neq 0$
2. $f’’(x)$连续
3. $x_0$足够接近解

应用

使用牛顿法求解开普勒方程$f(E)=E-M-e\sin E=0$。

E = M;
i = 0;
    
while ( abs(E-E_ref)> 1e-10 )
    i = i+1;
    E = E - (E-e*sin(E)-M)/(1-e*cos(E)); 
    fprintf('%3d ', i);
    fprintf('%16.11f ', E);
    fprintf('%11.2e ', abs(E-E_ref));
    fprintf('%6d \n', 2*i);          
end

Reference

---

1. Wiki about Newton method ↩