BP网络权值更新公式

BP网络又叫做误差反向传播网络，说这么复杂，从控制理论的角度来说，这玩意儿不就是一个负反馈回路么，无非是在负反馈回路中加入了一些自适应参数调整，不得不说有些时候还是控制科学与工程的名词叫起来更顺耳一些。BP这个负反馈过程实际上就是对权值进行更新的一个方法。本文参考了斯坦福大学的CNN for visual recognition课程，国外的这些个课程设计的简直碾压国内高校课程，看看配套的网站支持就知道了。斯坦福CNN for visual recognition课程。

预备知识

梯度： $\nabla f=[\frac{\partial f}{\partial x} ,\frac{\partial f}{\partial y}]$ ，即偏导数组成的向量。（在感叹一句，这课程简直太详细了，完全把学生当作一张白纸，从最基本的梯度概念开始讲起）。
链式法则： $\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}$ 。

了解了这两个基本的知识后，我们来搭建一个简单的神经网络，设 $f(x,y,z)=(x+y)z$ ，令$q=x+y$，则$f=qz$，令$x=-2,y=5,z=-4$，相应的几个函数输出及偏导数分别为：

$f=-12\\ q=3\\ \frac{\partial f}{\partial x}=z=-4\\ \frac{\partial f}{\partial y}=z=-4\\ \frac{\partial f}{\partial z}=(x+y)=3\\ \frac{\partial f}{\partial q}=z=-4\\ \frac{\partial q}{\partial x}=1\\ \frac{\partial q}{\partial y}=1$

用门电路的方式表示一下，下图中绿色的部分，就是网络计算的输出，它是前馈的，而红色就是$f$对各个分量进行求导得到的数值，它的方向正好是反馈过来的，所以也叫反向传播。

通过上面的电路，我们发现每个门可以独立（即局部地）完成两件事：

前向输出的计算
反向传播即局部偏导数的计算（注意是局部）

一旦网络前向输出过程完成，那么最终$f$对各个分量的偏导数也就可知了，即全局偏导数就已知了。

链式规则在这里的作用就像是齿轮一样，将每一个部分连接在一起。

现在假设我们想要让输出$f$变大，那么由于我们的$q$导数为负，因此我们希望$q$尽可能小一些，根据链式法则继续往前推，我们知道$q$对于$x,y$的导数为$1$，而输出$f$对于$x,y$的导数为$-4$，那么我们的目标就达到了，如果我们减小$x,y$，由于$x,y$对$f$导数为负，此时乘法门的输出会增大，也就是说我们的输出会增大。

模块化：sigmoid函数

任何可微函数都可以充当门，同时我们也可以将多个门组合成一个大门来使用，例如我们的sigmoid函数，就组合了七种门。

$f\left ( w,x \right )=\frac{1}{1+e^{-\left ( w_0x_0+ w_1x_1+w_2\right )}}$

除了加法门、乘法门和最大门，还有下面四种：

倒数门、偏移门、指数门以及倍数门。

$f\left ( x \right )=\frac{1}{x}\rightarrow \frac{\mathrm{d} f}{\mathrm{d} x}=-1/x^{2}\\ f_c\left ( x \right )=c+x\rightarrow \frac{\mathrm{d} f}{\mathrm{d} x}=1\\ f\left ( x \right )=e^{x}\rightarrow \frac{\mathrm{d} f}{\mathrm{d} x}=e^{x}\\ f_a\left ( x \right )=ax\rightarrow \frac{\mathrm{d} f}{\mathrm{d} x}=a$

组合起来就是这个样子：

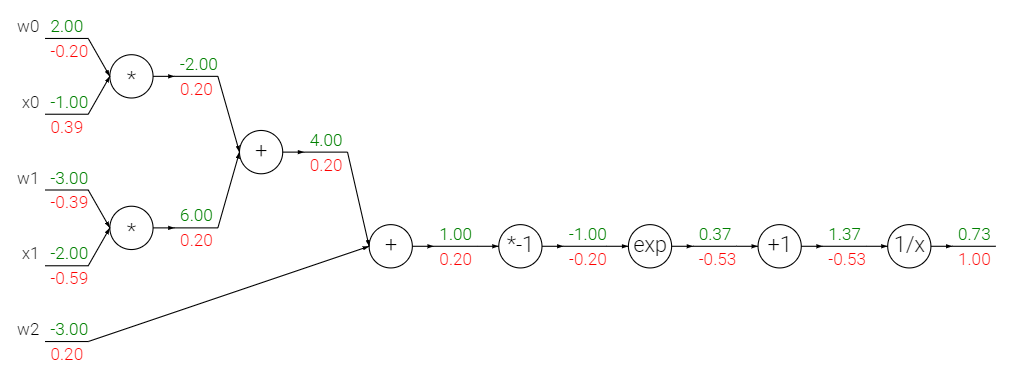
sigmoid函数会把输入向量轻柔地转换至0-1之间的一个数。

BP过程推导

那么我们现在进入重头戏，反向传播算法的推导。

1	`<iframe width="854" height="480" src="https://www.youtube.com/embed/xqf2DJgucsU" frameborder="0" allowfullscreen></iframe>`

多层单节点

考虑一个最简单的三层神经网络，它是下面这个样子：

输入、隐含和输出层每一个神经元包含权重$w$和偏置$b$，所以这个神经网络的cost function可以描述为：

$C(w_1,b_1,w_2,b_2,w_3,b_3)$

我们需要知道cost function对各个参数的敏感程度，这样我们就能知道调节那个参数可以最有效果地降低cost function。我们先考虑后两层神经元，即隐含层和输出层，同时令期望输出为1。这里的$L$上标代表层位置

那么我们输出层的代价函数就是：

$C_0(...)=(a^{(L)}-y)^2$

$a^{(L)}$是多少呢：

$a^{(L)}=\sigma(w^{(L)}a^{(L-1)}+b^{(L)})=\sigma(z^{(L)})\\ z^{(L)}=w^{(L)}a^{(L-1)}+b^{(L)}$

$\sigma$代表某种非线性函数，这里是上面提到的sigmoid函数。那么我们的计算关系树就如下图所示：

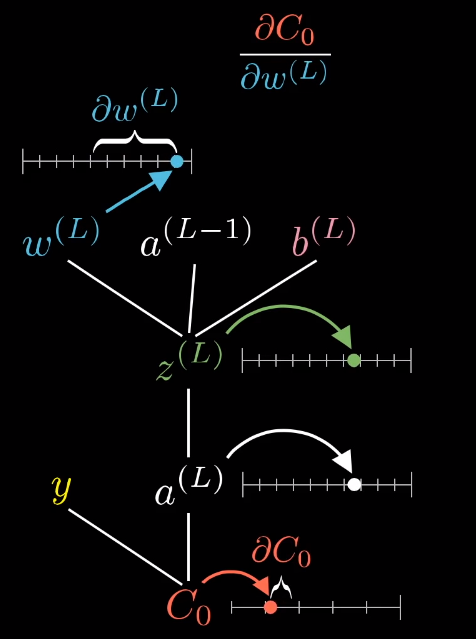
我们想要找到的是$C_0$和$w^{(L)}$之间的关系，就是求$\frac{\partial C_0}{\partial w^{\left ( L \right )}}$。那么怎么搞呢？用我们前面提到的链式法则。

$\frac{\partial C_0}{\partial w^{\left ( L \right )}}= \frac{\partial z^{(L)}}{\partial w^{\left ( L \right )}} \frac{\partial a^{(L)}}{\partial z^{\left ( L \right )}} \frac{\partial C_0}{\partial a^{\left ( L \right )}}\\ \frac{\partial C_0}{\partial a^{\left ( L \right )}}=2(a^{(L)}-y)\\ \frac{\partial a^{(L)}}{\partial z^{\left ( L \right )}}={\sigma}'(z^{(L)})\\ \frac{\partial z^{(L)}}{\partial w^{\left ( L \right )}}=a^{(L-1)}$

代入化简我们可以得到下面的式子：

$\frac{\partial C_0}{\partial w^{\left ( L \right )}}=2(a^{(L)}-y) {\sigma}'(z^{(L)}) a^{(L-1)}$

对于所有输入的训练样本：

$\frac{\partial C}{\partial w^{\left ( L \right )}}= \frac{1}{n} \sum_{k=0}^{n-1}\frac{\partial C_k}{\partial w^{\left ( L \right )}}$

其中$n$为样本数量，可以看到代价函数对$w$的导数是每一个样本输出值的均值。那么我们的整个网络的代价函数梯度可以写为：

$\nabla C=\begin{bmatrix} \frac{\partial C}{\partial w^{\left ( 1 \right )}}\\ \frac{\partial C}{\partial b^{\left ( 1 \right )}}\\ \vdots \\ \frac{\partial C}{\partial w^{\left ( L \right )}}\\ \frac{\partial C}{\partial b^{\left ( L \right )}} \end{bmatrix}$

多层多节点

上面讨论了多层神经网络，每层只有一个神经元，这一节咱们讨论一下多层多节点的复杂神经网络，实际上就是公式变得复杂了一些，道理是一样的。

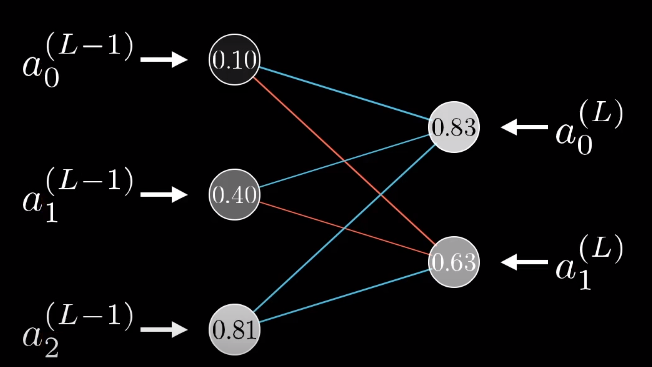
这里引入了下标，代表第$i$个神经元，我们的代价函数变为：

$C_0=\sum_{j=0}^{n_L-1}(a_j^{(L)}-y_j)^2$

我们令从第$k$个神经元到第$j$个神经元的权值为$w_{kj}^{(L)}$，那么我们的$z_j$则表示为：

$z_j^{(L)}=\sum_{k=0}^{n_L-1}w_{kj}^{(L)}a_k^{(L-1)}+b_j^{(L)}$

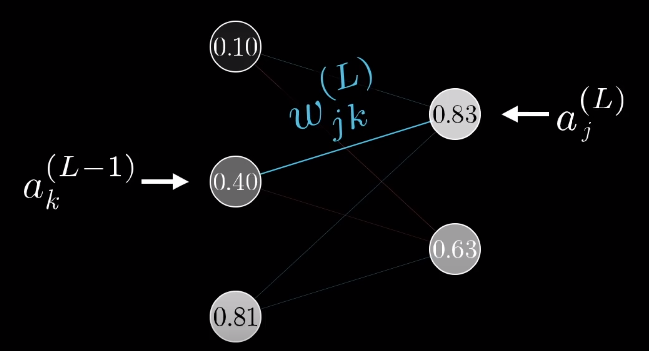
对应的，我们要激活第$L$层第$j$个神经元，其输出为$\sigma(z_j^{(L)})$。最终我们的代价函数对每一个权值的偏导数可以写为：

$\frac{\partial C_0}{\partial w_{jk}^{\left ( L \right )}}= \frac{\partial z_j^{(L)}}{\partial w_{jk}^{\left ( L \right )}} \frac{\partial a_j^{(L)}}{\partial z_j^{\left ( L \right )}} \frac{\partial C_0}{\partial a_j^{\left ( L \right )}}\\$

可以看出对每个权值的偏导数是没有变化的，多神经元与单神经元的区别是对上层输出的偏导数会发生变化：

$\frac{\partial C_0}{\partial a_{k}^{\left ( L \right )}}= \sum_{j=0}^{n_L-1} \frac{\partial z_j^{(L)}}{\partial a_{k}^{\left ( L-1 \right )}} \frac{\partial a_j^{(L)}}{\partial z_j^{\left ( L \right )}} \frac{\partial C_0}{\partial a_j^{\left ( L \right )}}\\$

讲到这里，基本上就可以算是把反向传播算法的基本原理写完了。后面有什么再接着补充。